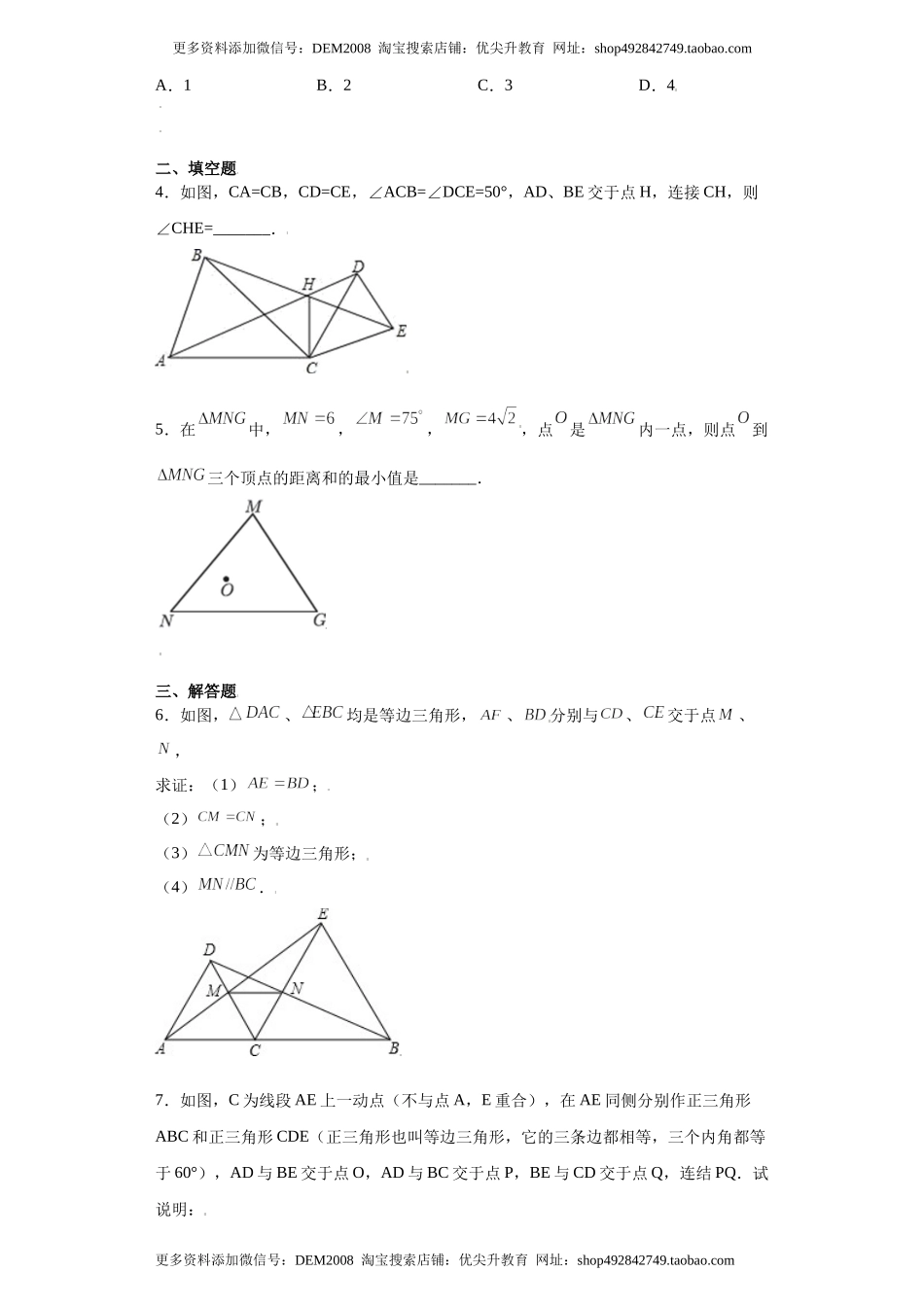
专题03模型方法课之手拉手模型压轴题专练(原卷版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM,下列结论:①△AOC≌△BOD;②AC=BD;③∠AMB=40°;④MO平分∠BMC.其中正确的个数为()A.4B.3C.2D.12.如图,,,三点在同一直线上,,都是等边三角形,连接,,:下列结论中正确的是()①△ACD≌△BCE;②△CPQ是等边三角形;③平分;④△BPO≌△EDO.A.①②B.①②③C.①②④D.①②③④3.如图,点C是线段AE上一动点(不与A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,有以下5个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中一定成立的结论有()个更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.com更多资料添加微信号:DEM2008淘宝搜索店铺:优尖升教育网址:shop492842749.taobao.comA.1B.2C.3D.4二、填空题4.如图,CA=CB,CD=CE,∠ACB=∠DCE=50°,AD、BE交于点H,连接CH,则∠CHE=_______.5.在中,,,,点是内一点,则点到三个顶点的距离和的最小值是_______.三、解答题6.如图,、均是等边三角形,、分别与、交于点、,求证:(1);(2);(3)为等边三角形;(4).7.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE(正三角形也叫等边三角形,它的三条边都相等,三个内角都等于60°),AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.试说明:(1)AD=BE;(2)填空∠AOE=°;(3)CP=CQ;8.如图1,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连结BE.(1)求证:△ACD≌△BCE;(2)图2,延长BE至Q,P为BQ上一点,连结CP,CQ使CP=CQ=5,若BC=8时,求PQ的长.9.如图1,点是线段上除点、外的任意一点,分别以、为边在线段的同旁做等边三角形和等边三角形,连接和BC相交于点Q,(1)求证:.(2)求的度数.(3)如图2所示,和仍为等边三角形,但和不在同一条直线上,是否成立,的度数与图1是否相等,请直接写出结论.10.在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE(顶点A、D、E按逆时针方向排列),且∠DAE=90°,AD=AE,连接...