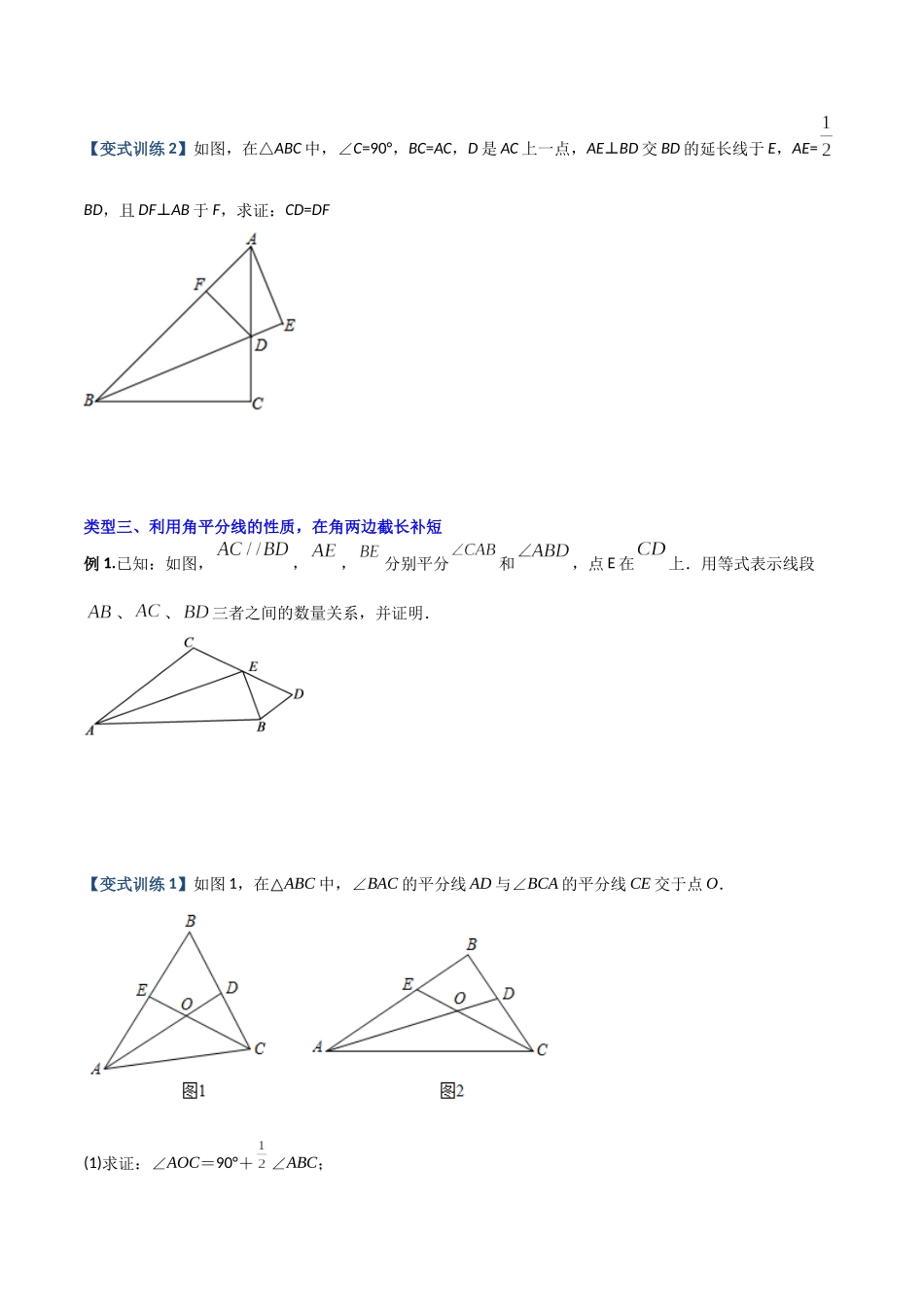
专题03与角平分线有关的辅助线的三种考法类型一、角平分线上的点向两边作垂线例1.如图,已知,P是的平分线上的任意一点,交于点D,于点E,如果,求的长.【变式训练1】如图,中,,点分别在边,上,,.求证:平分.【变式训练2】图,已知AE⊥AB,AF⊥AC.AE=AB,AF=AC,BF与CE相交于点M.(1)EC=BF;(2)EC⊥BF;(3)连接AM,求证:AM平分∠EMF.【变式训练3】已知点C是∠MAN平分线上一点,∠BCD的两边CB、CD分别与射线AM、AN相交于B,D两点,且∠ABC+∠ADC=180°.过点C作CE⊥AB,垂足为E.(1)如图1,当点E在线段AB上时,求证:BC=DC;(2)如图2,当点E在线段AB的延长线上时,探究线段AB、AD与BE之间的等量关系;(3)如图3,在(2)的条件下,若∠MAN=60°,连接BD,作∠ABD的平分线BF交AD于点F,交AC于点O,连接DO并延长交AB于点G.若BG=1,DF=2,求线段DB的长.类型二、过边上的点向角平分线作垂线构造等腰三角形例1.如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为______cm2.【变式训练1】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CEBD⊥,交BD的延长线于点E,若BD=4,则CE=________.【变式训练2】如图,在△ABC中,∠C=90°,BC=AC,D是AC上一点,AE⊥BD交BD的延长线于E,AE=BD,且DF⊥AB于F,求证:CD=DF类型三、利用角平分线的性质,在角两边截长补短例1.已知:如图,,,分别平分和,点E在上.用等式表示线段、、三者之间的数量关系,并证明.【变式训练1】如图1,在△ABC中,∠BAC的平分线AD与∠BCA的平分线CE交于点O.(1)求证:∠AOC=90°+∠ABC;(2)当∠ABC=90°时,且AO=3OD(如图2),判断线段AE,CD,AC之间的数量关系,并加以证明.【变式训练2】如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.(提示:过点E作EF⊥AD,垂足为F.)【变式训练3】如图所示,已知B(﹣2,0),C(2,0),A为y轴正半轴上的一点,点D为第二象限一动点,点E在BD的延长线上,CD交AB于点F,且∠BDC=∠BAC.(1)求证:∠ABD=∠ACD;(2)求证:AD平分∠CDE;(3)若在D点运动的过程中,始终有DC=DA+DB,在此过程中,∠BAC的度数是否发生变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数.【变式训练4】已知:如图1,在中,是的平分线.E是线段上一点(点E不与点A,点D重合),满足.(1)如图2,若,且,则________,_______.(2)求证:.(3)...