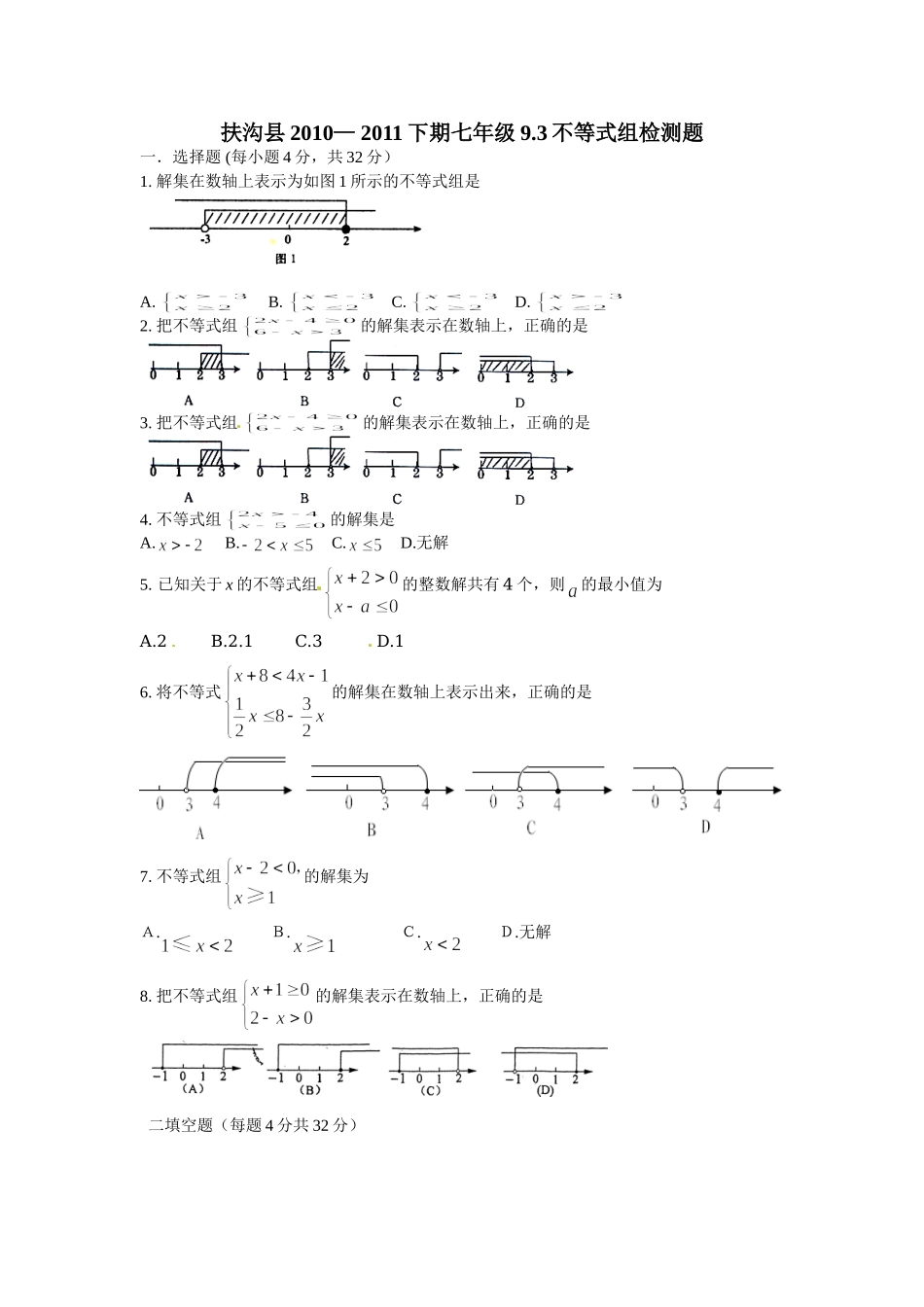
扶沟县2010—2011下期七年级9.3不等式组检测题一.选择题(每小题4分,共32分)1.解集在数轴上表示为如图1所示的不等式组是A.B.C.D.2.把不等式组的解集表示在数轴上,正确的是3.把不等式组的解集表示在数轴上,正确的是4.不等式组的解集是A.B.C.D.无解5.已知关于x的不等式组的整数解共有4个,则的最小值为A.2B.2.1C.3D.16.将不等式的解集在数轴上表示出来,正确的是7.不等式组的解集为A.B.C.D.无解8.把不等式组的解集表示在数轴上,正确的是二填空题(每题4分共32分)9.不等式组的整数解是.10.不等式组的解集为_______。11.若不等式组有三个整数解,则的取值范围为_____12.不等式组的整数解是_______________________13.不等式组212mxmx的解集是x<m-2,则m的取值应为_________。14.如果不等式组的解集是,那么的值为.15.关于x的不等式(5–2m)x>-3的解是正数,那么m所能取的最小整数是__________。16.比较下面两个算式结果是的大小(在横线上填“>、<、=”)______2×3×4______2×2×2______2×(—2)×5通过观察归纳,写出能反映这种规律的一般情况___________三.解答题(共36分)17.解不等式组,并把其解集在数轴上表示出来;(6分)18.已知,且,求x的取值范围。(6分)19.解不等式组,并写出不等式组的正整数解。(6分)20.青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元。(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价-进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案:(10分)21.2007年我市某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个种造型需甲种花卉80盆,乙种花卉40盆,搭配一个种造型需甲种花卉50盆,乙种花卉90盆.(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.(2)若搭配一个种造型的成本是800元,搭配一个种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?(10分)12345678DAABACAC1.[解析]本题考查了在数轴上表示不等式解集的方法,题目较简单.本题要注意区别“O”和“●”表示的不同含义,正确选好不等号。2.[解析]本题考查了用数轴表示不...