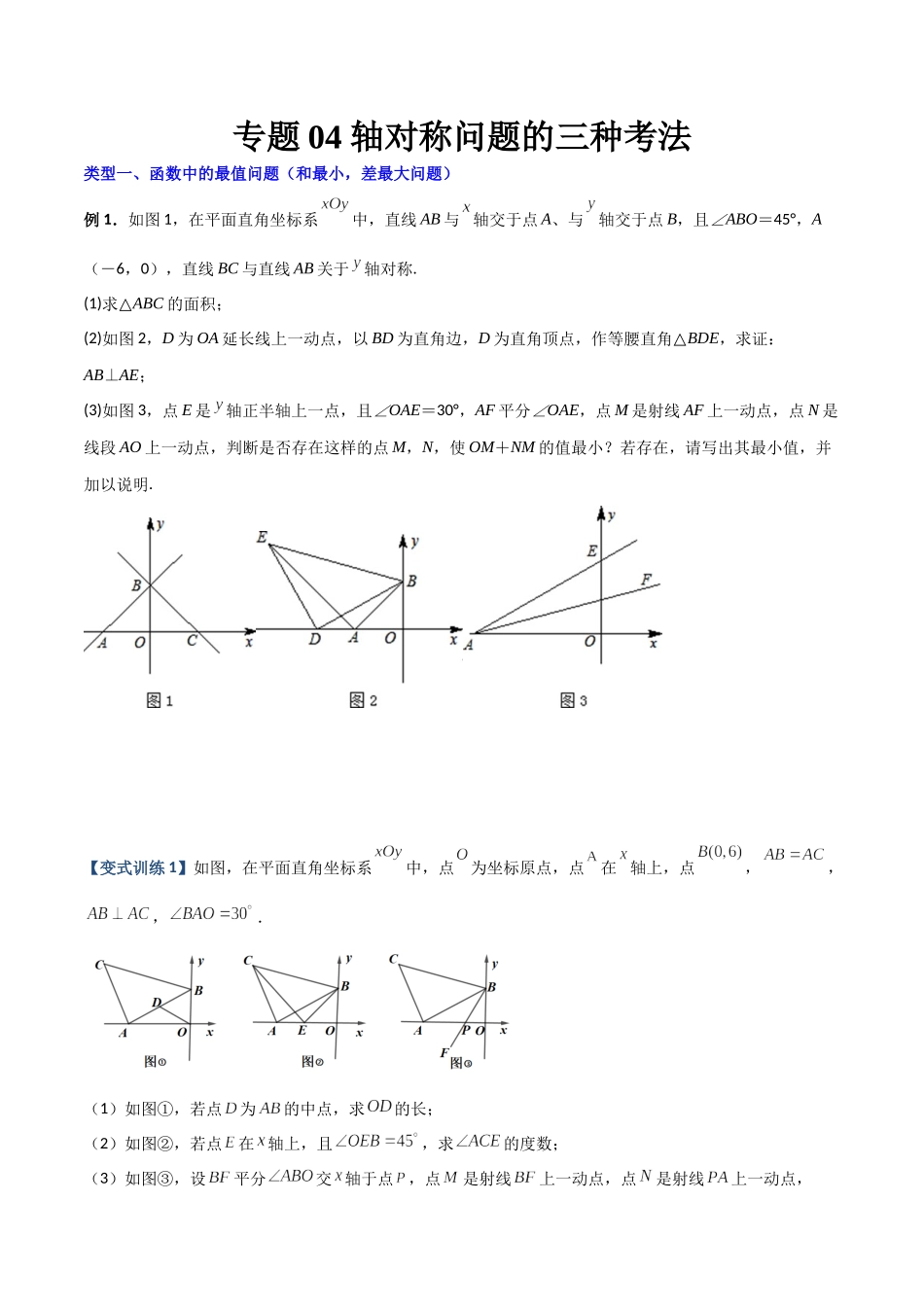
专题04轴对称问题的三种考法类型一、函数中的最值问题(和最小,差最大问题)例1.如图1,在平面直角坐标系中,直线AB与轴交于点A、与轴交于点B,且∠ABO=45°,A(-6,0),直线BC与直线AB关于轴对称.(1)求△ABC的面积;(2)如图2,D为OA延长线上一动点,以BD为直角边,D为直角顶点,作等腰直角△BDE,求证:AB⊥AE;(3)如图3,点E是轴正半轴上一点,且∠OAE=30°,AF平分∠OAE,点M是射线AF上一动点,点N是线段AO上一动点,判断是否存在这样的点M,N,使OM+NM的值最小?若存在,请写出其最小值,并加以说明.【变式训练1】如图,在平面直角坐标系中,点为坐标原点,点在轴上,点,,,.(1)如图①,若点为的中点,求的长;(2)如图②,若点在轴上,且,求的度数;(3)如图③,设平分交轴于点,点是射线上一动点,点是射线上一动点,的最大值为,判断是否存在这样点,,使的值最小?若存在,请在答题卷上作出点,,并直接写出作法和的最小值;若不存在,请说明理由.【变式训练2】在平面直角坐标系中,B(2,2),以OB为一边作等边△OAB(点A在x轴正半轴上).(1)若点C是y轴上任意一点,连接AC,在直线AC上方以AC为一边作等边△ACD.①如图1,当点D落在第二象限时,连接BD,求证:ABBD⊥;②若△ABD是等腰三角形,求点C的坐标;(2)如图2,若FB是OA边上的中线,点M是FB一动点,点N是OB一动点,且OM+NM的值最小,请在图2中画出点M、N的位置,并求出OM+NM的最小值.【变式训练3】如图,在平面直角坐标系中,点为坐标原点,点在轴上,点,,,.(1)如图①,若点为的中点,求的长;(2)如图②,若点在轴上,且,求的度数;(3)如图③,设平分交轴于点,点是射线上一动点,点是射线上一动点,的最大值为,判断是否存在这样点,,使的值最小?若存在,请在答题卷上作出点,,并直接写出作法和的最小值;若不存在,请说明理由.类型二、几何图形中的最短路径问题例.已知点在内.(1)如图1,点关于射线的对称点是,点关于射线的对称点是,连接、、.①若,则______;②若,连接,请说明当为多少度时,;(2)如图2,若,、分别是射线、上的任意一点,当的周长最小时,求的度数.【变式训练1】如图,将边长为的正三角形纸片按如下顺序进行两次折叠,展开后,得折痕(如图①),点为其交点.(1)探求与的数量关系,并说明理由;(2)如图②,若分别为上的动点.①当的长度取得最小值时,求的长度;②如图③,若点在线段上,,则的最小值=.【变式...