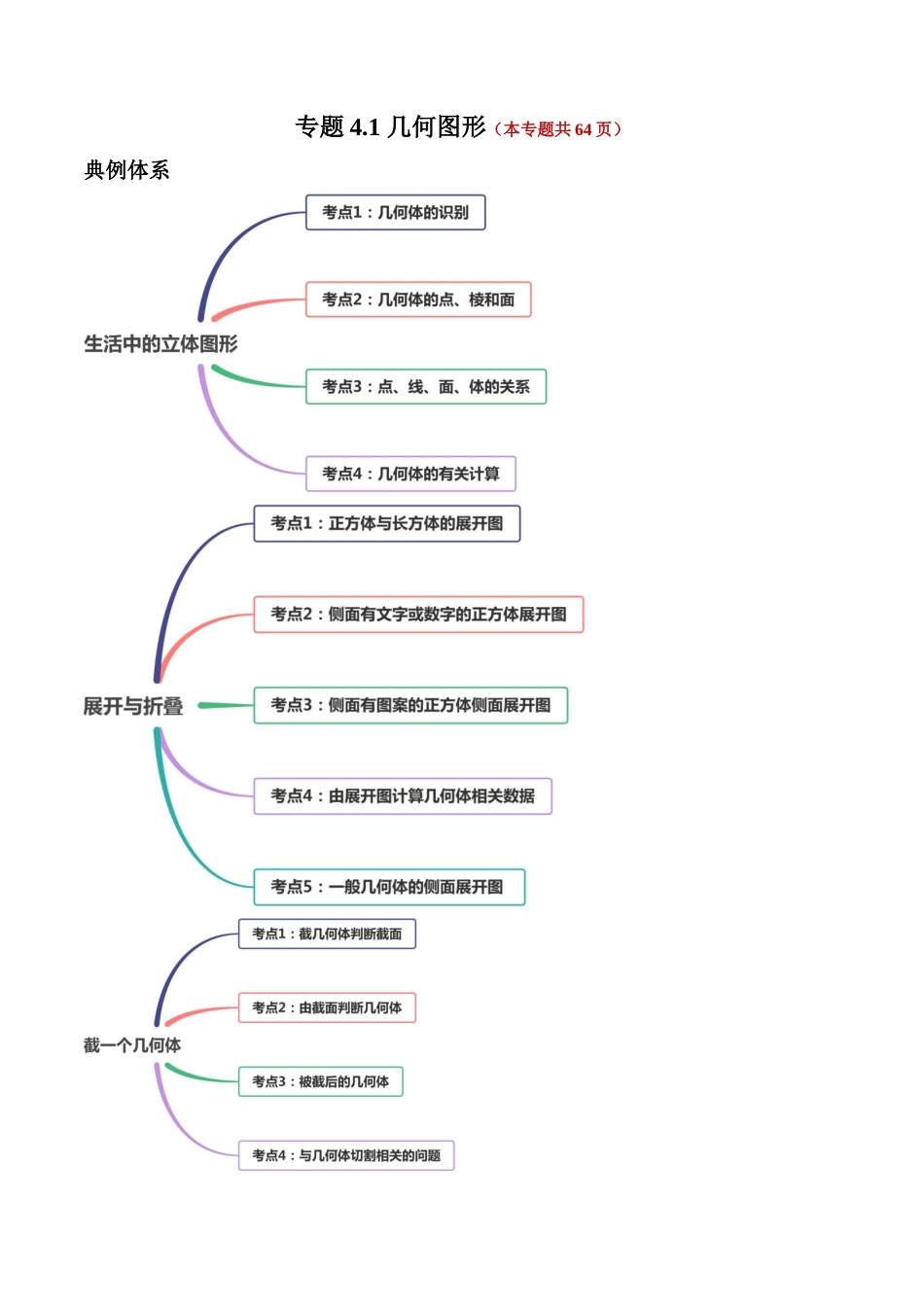
专题4.1几何图形(本专题共64页)典例体系一、知识点1.立体图形与平面图形从实物中抽象出来的各种图形,包括立体图形和平面图形。立体图形:有些几何图形的各个部分不都在同一平面内,它们是立体图形。平面图形:有些几何图形的各个部分都在同一平面内,它们是平面图形。2、点、线、面、体(1)几何图形的组成点:线和线相交的地方是点,它是几何图形中最基本的图形。线:面和面相交的地方是线,分为直线和曲线。面:包围着体的是面,分为平面和曲面。体:几何体也简称体。(2)点动成线,线动成面,面动成体。3、生活中的立体图形4、棱柱及其有关概念:棱:在棱柱中,任何相邻两个面的交线,都叫做棱。侧棱:相邻两个侧面的交线叫做侧棱。n棱柱有两个底面,n个侧面,共(n+2)个面;3n条棱,n条侧棱;2n个顶点。棱柱的所有侧棱长都相等,棱柱的上下两个底面是相同的多边形,直棱柱的侧面是长方形。棱柱的侧面有可能是长方形,也有可能是平行四边形。5、正方体的平面展开图:11种6、截一个正方体:用一个平面去截一个正方体,截出的面可能是三角形,四边形,五边形,六边形。7、三视图物体的三视图指主视图、俯视图、左视图。主视图:从正面看到的图,叫做主视图。左视图:从左面看到的图,叫做左视图。俯视图:从上面看到的图,叫做俯视图。二、考点点拨与训练1、生活中的立体图形考点1:几何体的识别典例:(2019·江西省初三月考)下列几何体中,是圆柱的为A.B.C.D.【答案】A【解析】:A选项为圆柱,B选项为圆锥,C选项为四棱柱,D选项为四棱锥.故选A.方法或规律点拨考查立体图形的认识,掌握立体图形的特征是解题的关键.巩固练习1.(2019·河北省初一期末)下面几种图形:①三角形,②长方形,③立方体,④圆,⑤圆锥,⑥圆柱.其中属于立体图形的有()A.1个B.2个C.3个D.4个【答案】C【解析】解:根据以上分析:属于立体图形的是③立方体⑤圆锥⑥圆柱,共计3个.故选:C.2.(2020·贵州省初三学业考试)下列列举的物体中,与铅球的形状类似的是()A.音箱B.铅笔C.西瓜D.水杯【答案】C【解析】解:铅球的形状是球体.A.音箱是柱体,故不符合题意;B.铅笔是柱体,故不符合题意;C.西瓜是球体,符合题意;D.水杯是柱体,故不符合题意;故选C.3.(2020·浙江省初三学业考试)如图,一个正方体有盖盒子(可密封)里装入六分之一高度的水,改变正方体盒子的放置方式,下列选项中不是盒子里的水能形成的几何体是()A.正方体B.长...