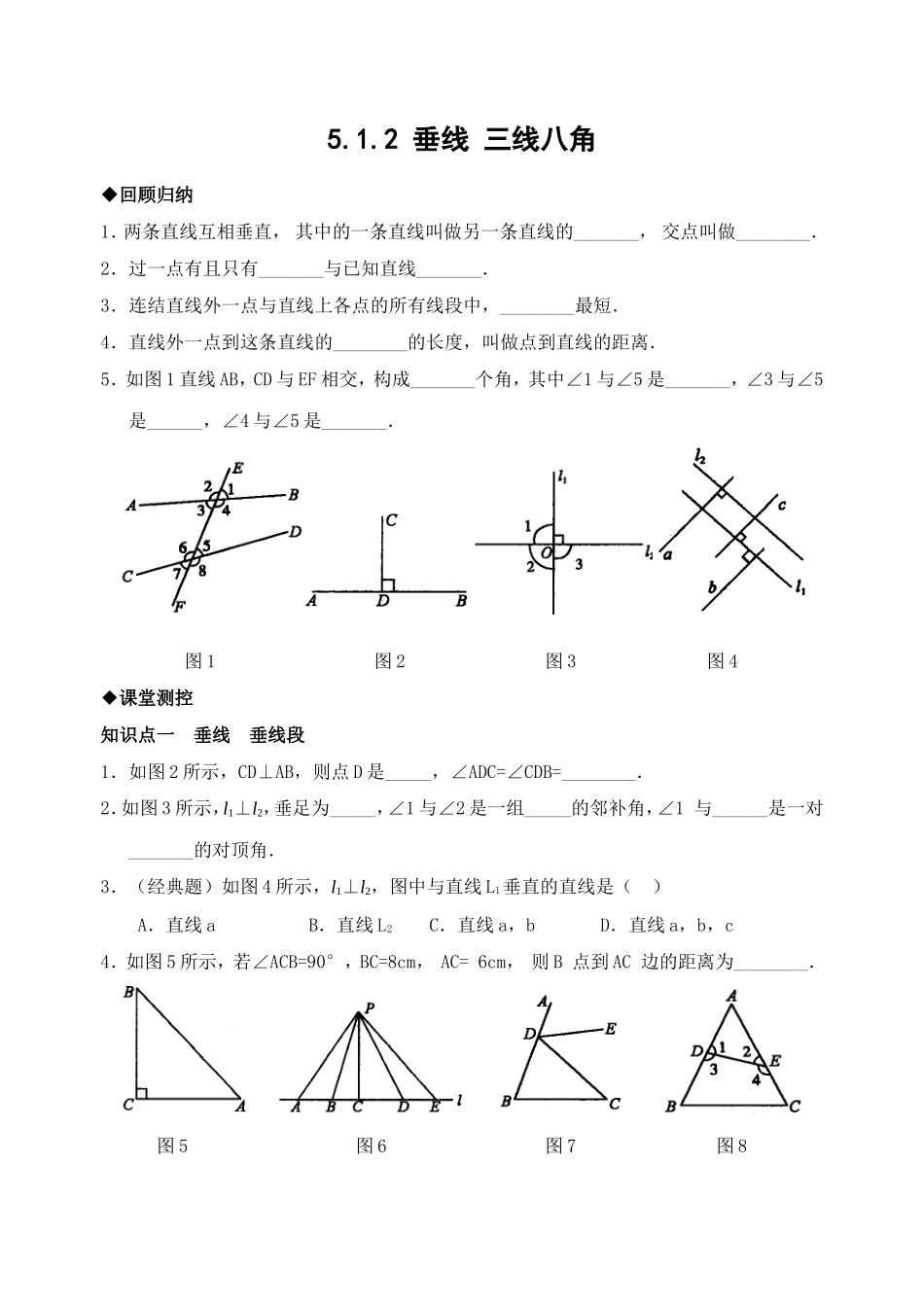
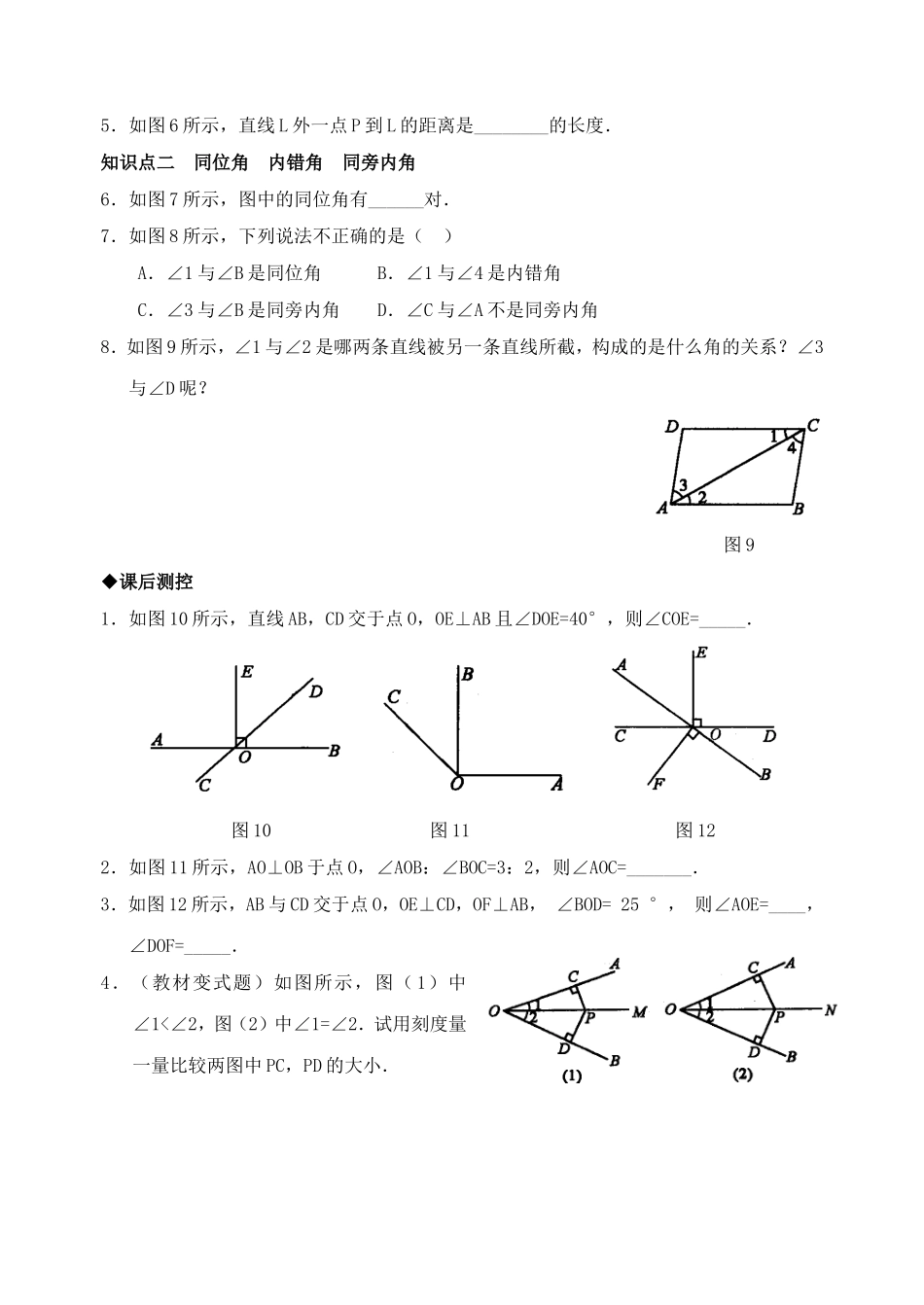
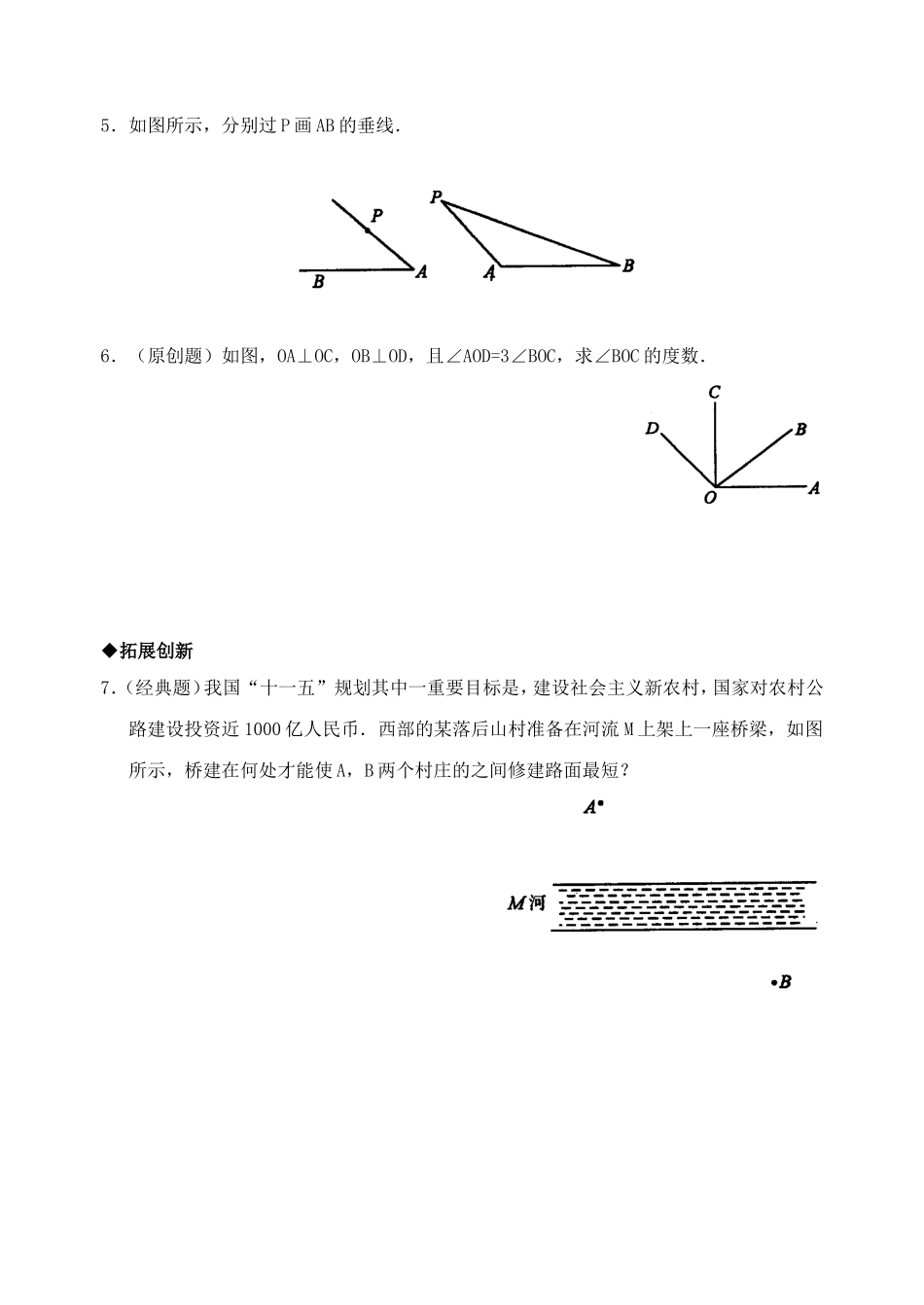
5.1.2垂线三线八角◆回顾归纳1.两条直线互相垂直,其中的一条直线叫做另一条直线的_______,交点叫做________.2.过一点有且只有_______与已知直线_______.3.连结直线外一点与直线上各点的所有线段中,________最短.4.直线外一点到这条直线的________的长度,叫做点到直线的距离.5.如图1直线AB,CD与EF相交,构成_______个角,其中∠1与∠5是_______,∠3与∠5是______,∠4与∠5是_______.图1图2图3图4◆课堂测控知识点一垂线垂线段1.如图2所示,CD⊥AB,则点D是_____,∠ADC=∠CDB=________.2.如图3所示,l1⊥l2,垂足为_____,∠1与∠2是一组_____的邻补角,∠1与______是一对_______的对顶角.3.(经典题)如图4所示,l1⊥l2,图中与直线L1垂直的直线是()A.直线aB.直线L2C.直线a,bD.直线a,b,c4.如图5所示,若∠ACB=90°,BC=8cm,AC=6cm,则B点到AC边的距离为________.图5图6图7图85.如图6所示,直线L外一点P到L的距离是________的长度.知识点二同位角内错角同旁内角6.如图7所示,图中的同位角有______对.7.如图8所示,下列说法不正确的是()A.∠1与∠B是同位角B.∠1与∠4是内错角C.∠3与∠B是同旁内角D.∠C与∠A不是同旁内角8.如图9所示,∠1与∠2是哪两条直线被另一条直线所截,构成的是什么角的关系?∠3与∠D呢?图9◆课后测控1.如图10所示,直线AB,CD交于点O,OE⊥AB且∠DOE=40°,则∠COE=_____.图10图11图122.如图11所示,AO⊥OB于点O,∠AOB:∠BOC=3:2,则∠AOC=_______.3.如图12所示,AB与CD交于点O,OE⊥CD,OF⊥AB,∠BOD=25°,则∠AOE=____,∠DOF=_____.4.(教材变式题)如图所示,图(1)中∠1<∠2,图(2)中∠1=∠2.试用刻度量一量比较两图中PC,PD的大小.5.如图所示,分别过P画AB的垂线.6.(原创题)如图,OA⊥OC,OB⊥OD,且∠AOD=3∠BOC,求∠BOC的度数.◆拓展创新7.(经典题)我国“十一五”规划其中一重要目标是,建设社会主义新农村,国家对农村公路建设投资近1000亿人民币.西部的某落后山村准备在河流M上架上一座桥梁,如图所示,桥建在何处才能使A,B两个村庄的之间修建路面最短?答案:回顾归纳1.垂线,垂足2.一条直线,垂直3.垂线段4.垂线段5.八,同位角,内错角,同旁内角课堂测控1.垂足,90°2.O,相等,∠3,90°3.D(点拨: L1∥L2,a⊥L1,b⊥L1,c⊥L1)4.8cm(点拨:点到直线距离定义)5.PC的长(点拨:PE>PD>PC,PA>PB>PC)6.2(点拨:∠...