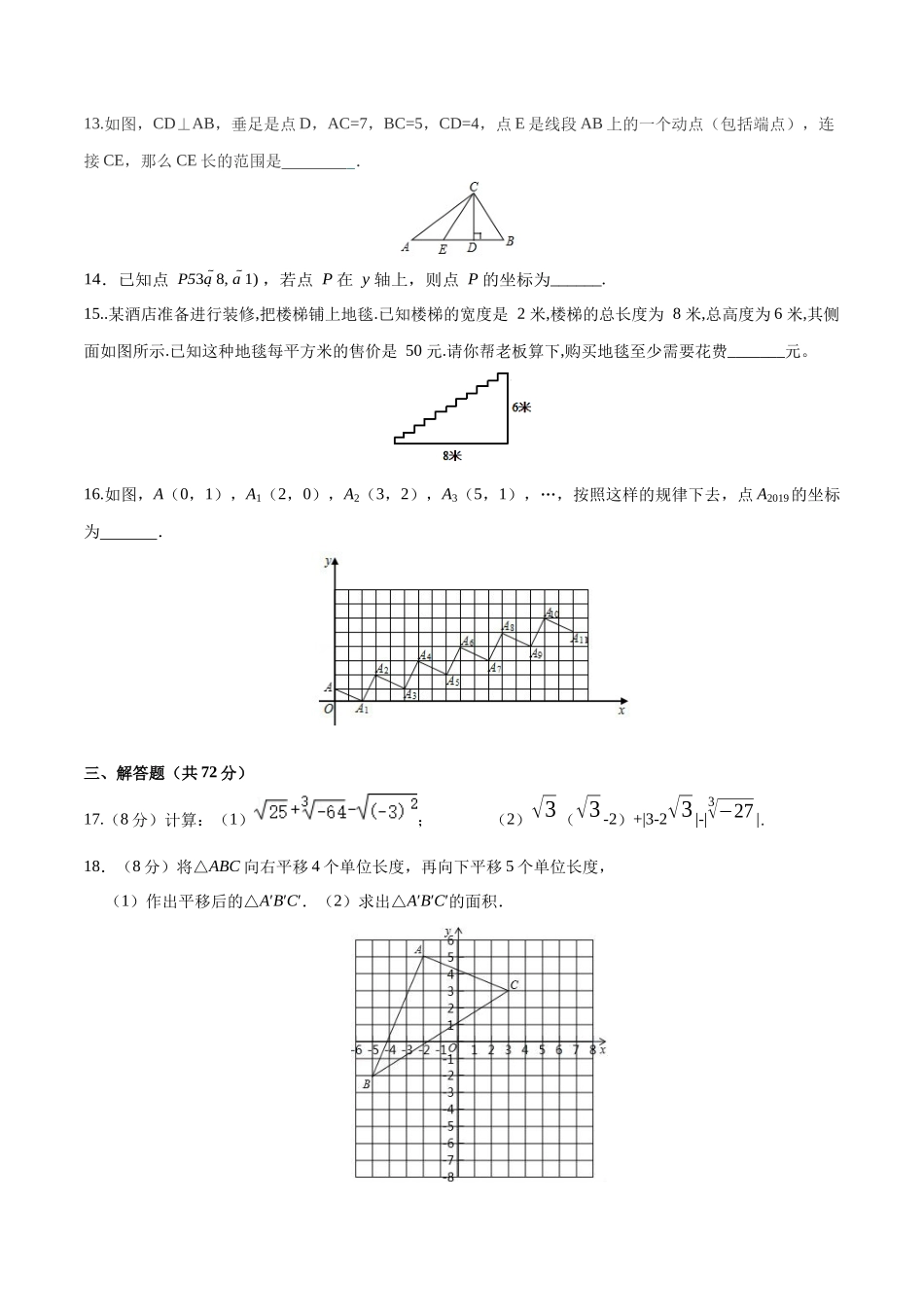
七年级数学下学期期中测试卷一、选择题(每小题3分,共36分)1.如图所示,下列条件中,能判断直线l1∥l2的是()A.∠2=∠3B.∠1=∠3C.∠4+∠5=180°D.∠2=∠42.在,0,,,,﹣1.414中,有理数有()A.1个B.2个C.3个D.4个3.如图三角形ABC平移后得到三角形DEF.若AE=11,DB=5,则平移的距离是()A.6B.3C.5D.114.与3+√8最接近的整数是()A.3B.4C.5D.65.如图,直线AB与CD相交于点O,∠1=∠2,若∠AOE=138°,则∠AOC的度数为()A.45°B.90°C.84°D.100°6.下列说法正确的是()A.1的平方根是1B.平方根是±4C.(﹣3)2的平方根是3D.4的算术平方根是27.若点P(a,b)在第二象限,则点Q(-b,1﹣a)所在象限应该是()A.第一象限B.第二象限C.第三象限D.第四象限8.①实数和数轴上的点一一对应;②不带根号的数一定是有理数;③一个数的立方根是它本身,这样的数有两个;④的算术平方根是9.其中真命题有()A.1个B.2个C.3个D.4个9.已知A(1,﹣3),B(2,﹣2),现将线段AB平移至A1B1,如果A1(a,1),B1(5,b),那么ab的值是()A.32B.16C.5D.410.如图,若∠1=∠2,DE∥BC,则下列结论正确的个数为()①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC.A.1个B.2个C.3个D.4个11.在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A2018的坐标为()A.(3,1)B.(0,4)C.(﹣3,1)D.(0,﹣2)12.如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有()A.1个B.2个C.3个D.4个二、填空题(每小题3分,共12分)13.如图,CD⊥AB,垂足是点D,AC=7,BC=5,CD=4,点E是线段AB上的一个动点(包括端点),连接CE,那么CE长的范围是.14.已知点P53a8,a1),若点P在y轴上,则点P的坐标为______.15..某酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,其侧面如图所示.已知这种地毯每平方米的售价是50元.请你帮老板算下,购买地毯至少需要花费_______元。16.如图,A(0,1),A1(2,0),A2(3...