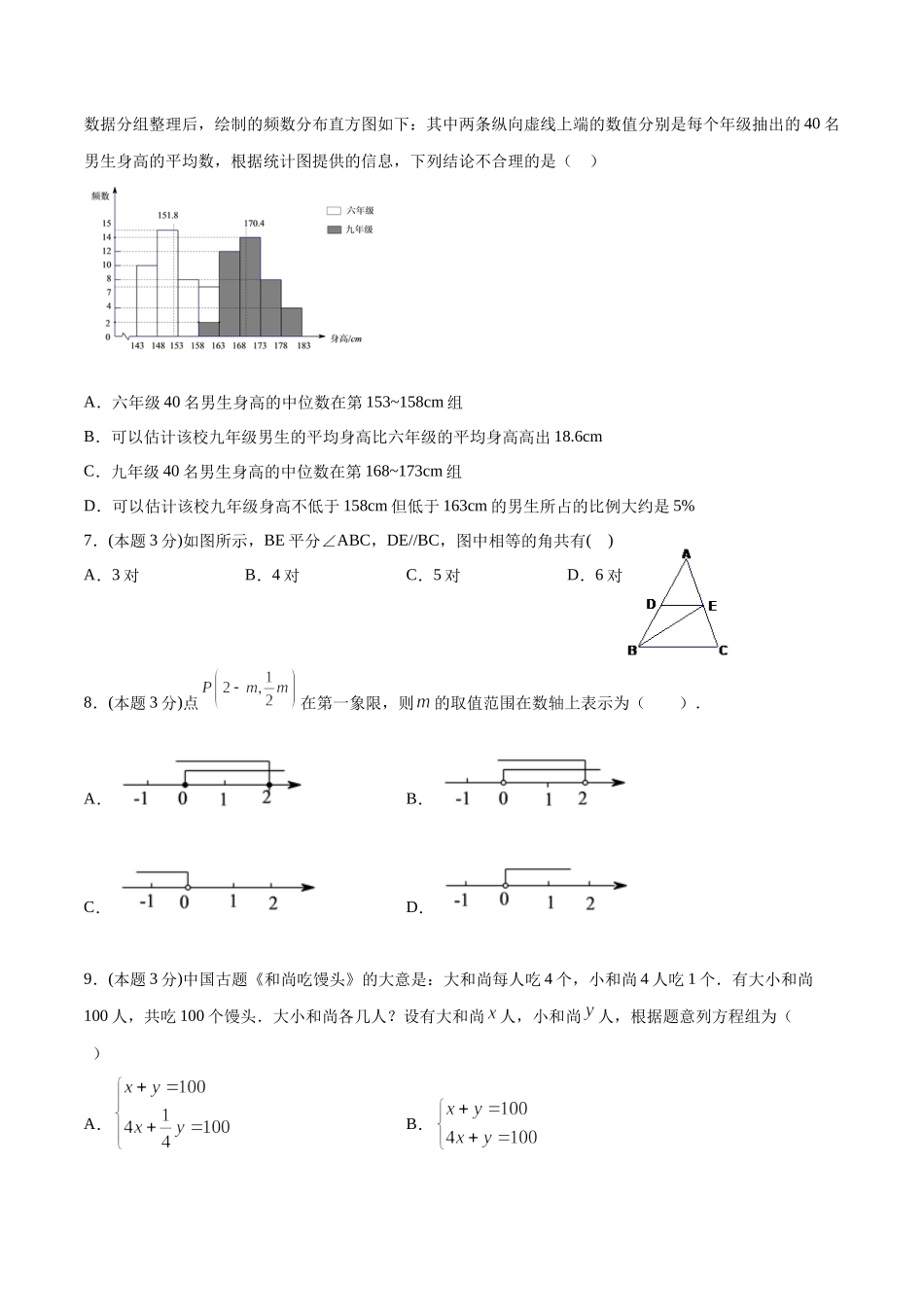
2020—2021年度下学期七年级期末全真模拟试题(五)数学试卷一、单选题(每小题3分,共30分)1.(本题3分)在下列汽车标志的图案中,能用图形的平移来分析其形成过程的是()A.B.C.D.2.(本题3分)下列说明错误的是()A.4的平方根是±2B.是分数C.是有理数D.是无理数3.(本题3分)下列语句正确的是()A.在平面直角坐标系中,与表示两个不同的点B.平行于轴的直线上所有点的横坐标都相同、C.若点在轴上,则D.点到轴的距离为34.(本题3分)二元一次方程组的解是A.B.C.D.5.(本题3分)已知关于x的方程2x-a=x-1的解是非负数,则a的取值范围为()A.B.C.D.6.(本题3分)某九年一贯制学校在六年级和九年级的男生中分别随机抽取40名学生测量他们的身高,将数据分组整理后,绘制的频数分布直方图如下:其中两条纵向虚线上端的数值分别是每个年级抽出的40名男生身高的平均数,根据统计图提供的信息,下列结论不合理的是()A.六年级40名男生身高的中位数在第153~158cm组B.可以估计该校九年级男生的平均身高比六年级的平均身高高出18.6cmC.九年级40名男生身高的中位数在第168~173cm组D.可以估计该校九年级身高不低于158cm但低于163cm的男生所占的比例大约是5%7.(本题3分)如图所示,BE平分∠ABC,DE//BC,图中相等的角共有()A.3对B.4对C.5对D.6对8.(本题3分)点在第一象限,则的取值范围在数轴上表示为().A.B.C.D.9.(本题3分)中国古题《和尚吃馒头》的大意是:大和尚每人吃4个,小和尚4人吃1个.有大小和尚100人,共吃100个馒头.大小和尚各几人?设有大和尚人,小和尚人,根据题意列方程组为()A.B.C.D.10.(本题3分)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点,第二次运动到点,第三次运动到,…,按这样的运动规律,第2022次运动后,动点的坐标是()A.B.C.D.二、填空题(每小题3分,共30分)11.(本题3分)写出一个比﹣3大的无理数______.12.(本题3分)若点到轴的距离是4,则的值是________.13.(本题3分)若x2m-1+5y3n-2m=7是二元一次方程,则m+n=________.14.(本题3分)若则____________15.(本题3分)同一平面内的三条直线,其交点的个数可能为________.16.(本题3分)四川雅安发生地震后,某校九(1)班学生开展献爱心活动,积极向灾区捐款.如图是该班同学捐款的条形统计图,写出一条你从图中所获得的信息:___.17.(本题3分)某种商品的进价为15元,出售时标价是22.5...