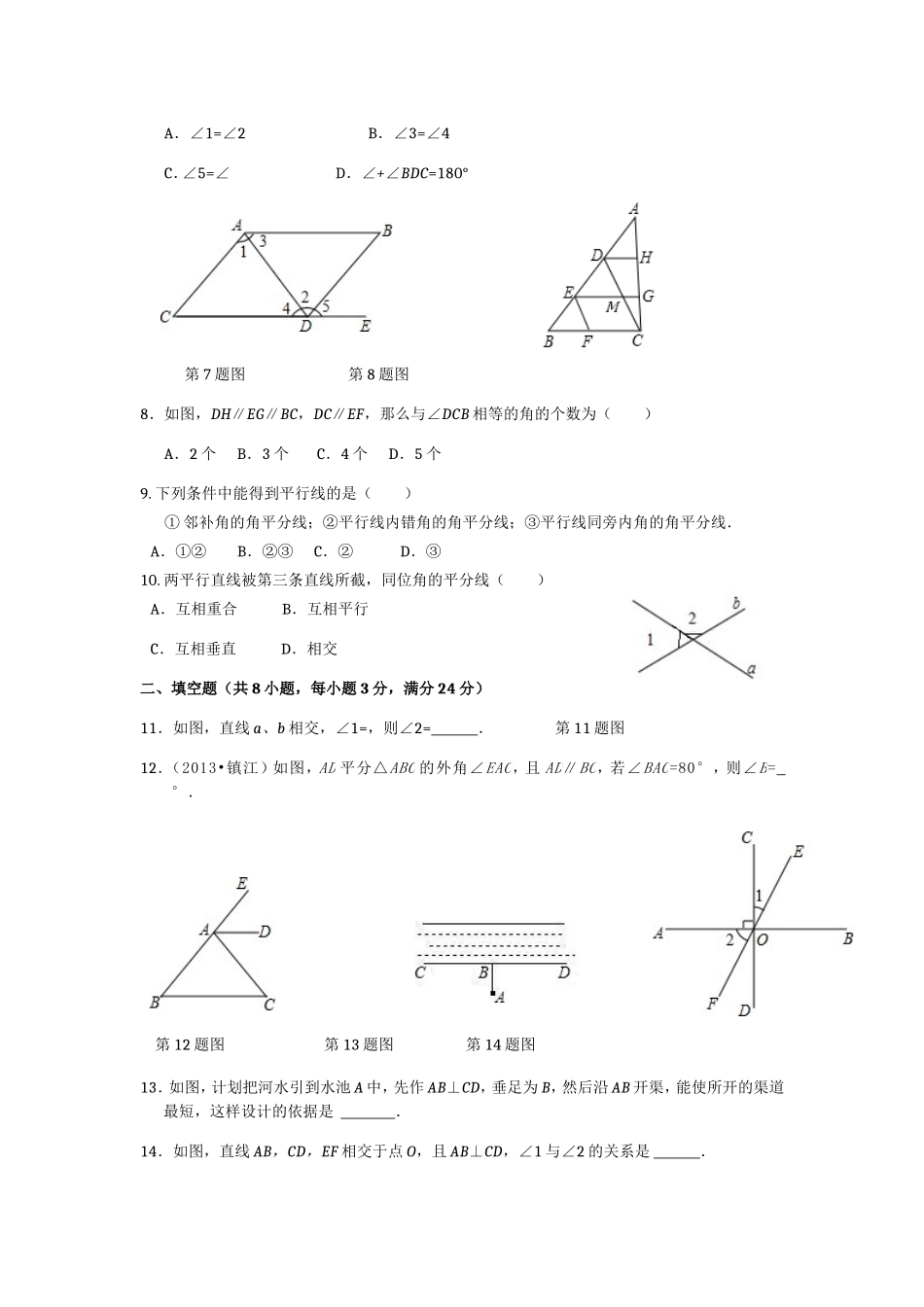
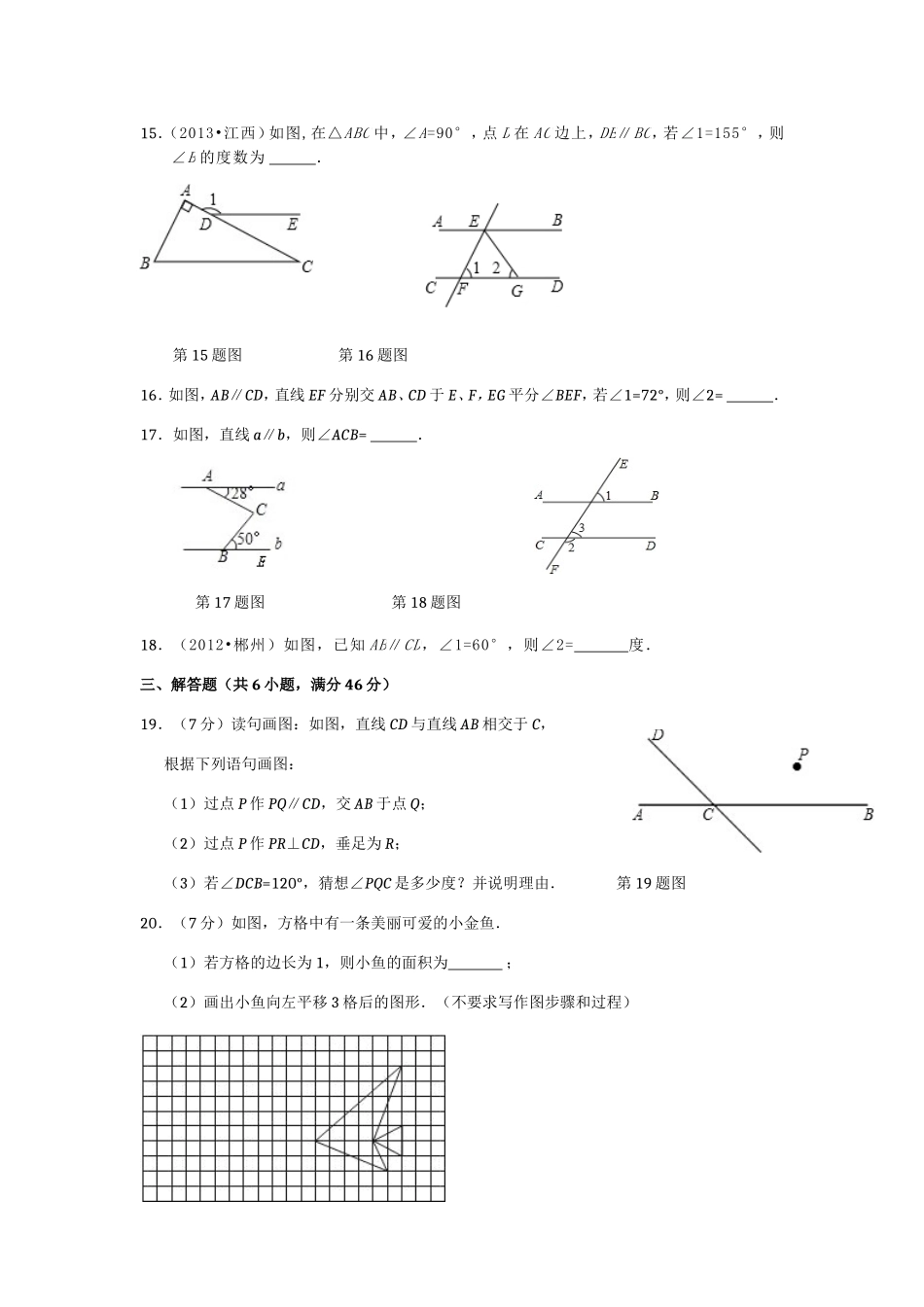
第五章相交线与平行线检测题(时间:90分钟,满分:100分)一、选择题(每小题3分,共30分)1.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中错误的有()A.1个B.2个C.3个D.4个2.点P是直线l外一点,A为垂足,,且PA=4cm,则点P到直线l的距离()A.小于4cmB.等于4cmC.大于4cmD.不确定3.(2013•安徽)如图,AB∥CD,∠A+∠E=75°,则∠C为()A.60°B.65°C.75°D.80°第3题图第4题图4.(2013•襄阳)如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的度数为()A.55°B.50°C.45°D.40°5.(2013•孝感)如图,∠1=∠2,∠3=40°,则∠4等于()A.120°B.130°C.140°D.40°6.如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有()A.1个B.2个C.3个D.4个第5题图第6题图7.如图,点在的延长线上,下列条件中不能判定AB∥CD的是()A.∠1=∠2B.∠3=∠4C.∠5=∠D.∠+∠BDC=180°第7题图第8题图8.如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为()A.2个B.3个C.4个D.5个9.下列条件中能得到平行线的是()①邻补角的角平分线;②平行线内错角的角平分线;③平行线同旁内角的角平分线.A.①②B.②③C.②D.③10.两平行直线被第三条直线所截,同位角的平分线()A.互相重合B.互相平行C.互相垂直D.相交二、填空题(共8小题,每小题3分,满分24分)11.如图,直线a、b相交,∠1=,则∠2=.第11题图12.(2013•镇江)如图,AD平分△ABC的外角∠EAC,且AD∥BC,若∠BAC=80°,则∠B=°.第12题图第13题图第14题图13.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是.14.如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是.15.(2013•江西)如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为.第15题图第16题图16.如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=.17.如图,直线a∥b,则∠ACB=.第17题图第18题图18.(2012•郴州)如图,已知AB∥CD,∠1=60°,则∠2=度.三、解答题(共6小题,满分46分)19.(7分)读句画图:如图,直线CD与直线AB相交于C,根据下列语句画图:(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.第19...