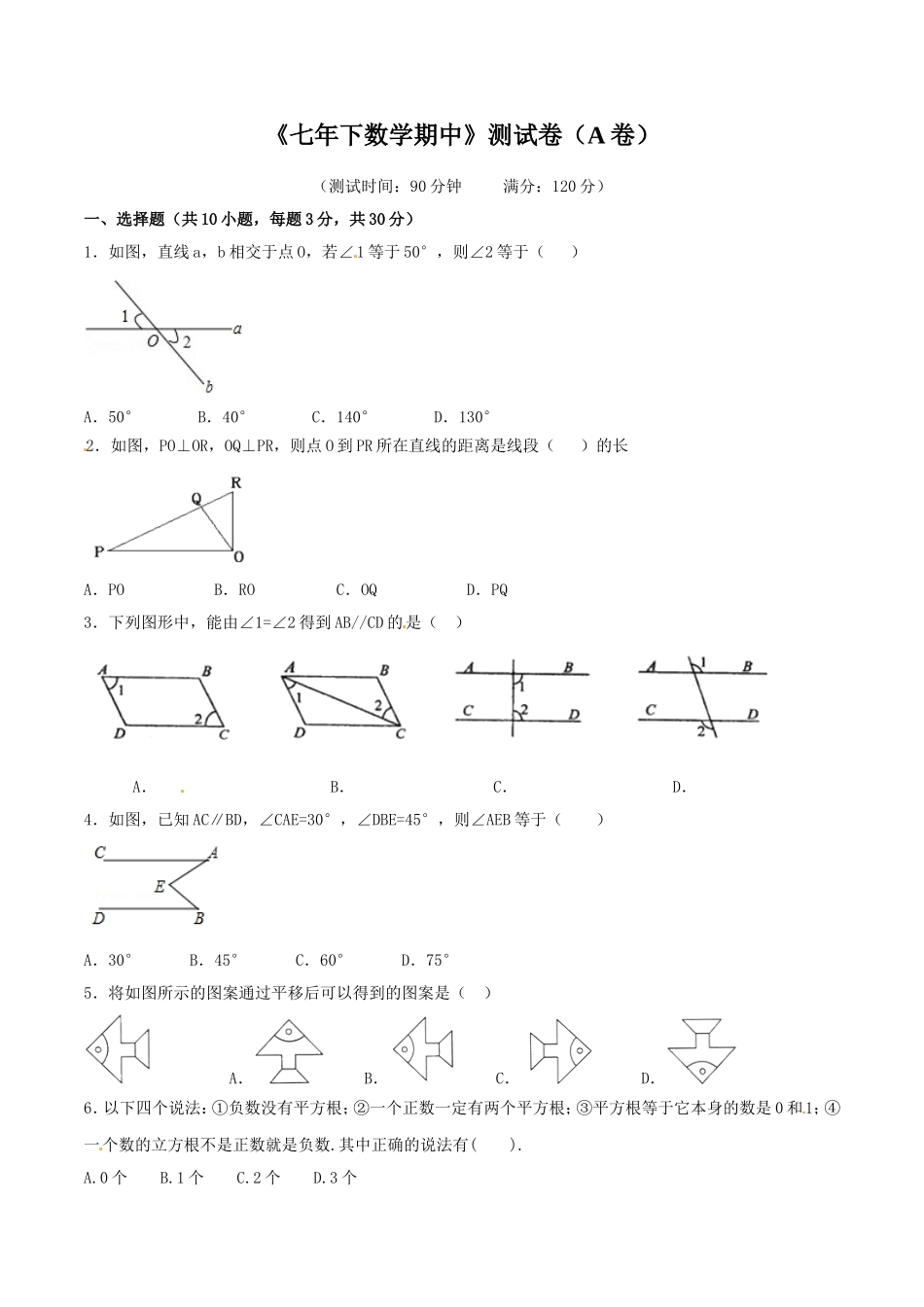
《七年下数学期中》测试卷(A卷)(测试时间:90分钟满分:120分)一、选择题(共10小题,每题3分,共30分)1.如图,直线a,b相交于点O,若∠1等于50°,则∠2等于()X§K]A.50°B.40°C.140°D.130°2.如图,PO⊥OR,OQ⊥PR,则点O到PR所在直线的距离是线段()的长A.POB.ROC.OQD.PQ3.下列图形中,能由∠1=∠2得到AB//CD的是()A.B.C.D.[来源:Zxxk.Com]4.如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB等于()A.30°B.45°C.60°D.75°5.将如图所示的图案通过平移后可以得到的图案是()A.B.C.D.6.以下四个说法:①负数没有平方根;②一个正数一定有两个平方根;③平方根等于它本身的数是0和1;④一个数的立方根不是正数就是负数.其中正确的说法有().A.0个B.1个C.2个D.3个7.在实数,-,,,-,,,中,无理数有().A.1个B.2个C.3个D.4个8.在平面直角坐标系中,已知点,则点在().A.第一象限B.第二象限C.第三象限D.第四象限9.在平面直角坐标系中,将点向右平移3个单位长度,再向上平移4个单位长度得到点的坐标是().A.B.C.D.10.如图是一局围棋比赛的几手棋.为记录棋谱方便,横线用数字表示,纵线用字母表示,这样,黑棋的位置可记为(B,2),白棋②的位置可记为(D,1),则白棋⑨的位置应记为()A.(C,5)B.(C,4)C.(4,C)D.(5,C)二、填空题(共10小题,每题3分,共30分)11.如图,若l1∥l2,∠1=50°,则∠2=°.12.如图,已知AB//DE,∠ABC=75°,∠CDE=150°,则∠BCD的度数为.13.如图,直线交于点,射线平分,若,则.MODCBA14.如图,已知AB∥CD,∠C=35°,BC平分∠ABE,则∠ABE的度数是15.81的平方根是;的立方根是.16.在直角坐标系中,点M(3,-5)到x轴的距离是_____.17.当a=______时,P(3a+1,a+4)在x轴上,到y轴的距离是______.[来源:Zxxk.Com]18.在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,8),A4(4,15),…,用你发现的规律确定点An的坐标为.19.第四象限内的点P到x轴的距离是3,到y轴的距离是5,则点P的坐标是;20.平面直角坐标系中有一点(1,1)A,对点A进行如下操作:第一步,作点A关于x轴的对称点1A,延长线段1AA到点2A,使得122AA=1AA;第二步,作点2A关于y轴的对称点3A,延长线段23AA到点4A,使得34232AAAA;第三步,作点4A关于x轴的对称点5A,延长线段45AA到点6A,使得56452AAAA;·······则点2A的坐标为________,点2014A的坐标为_______...