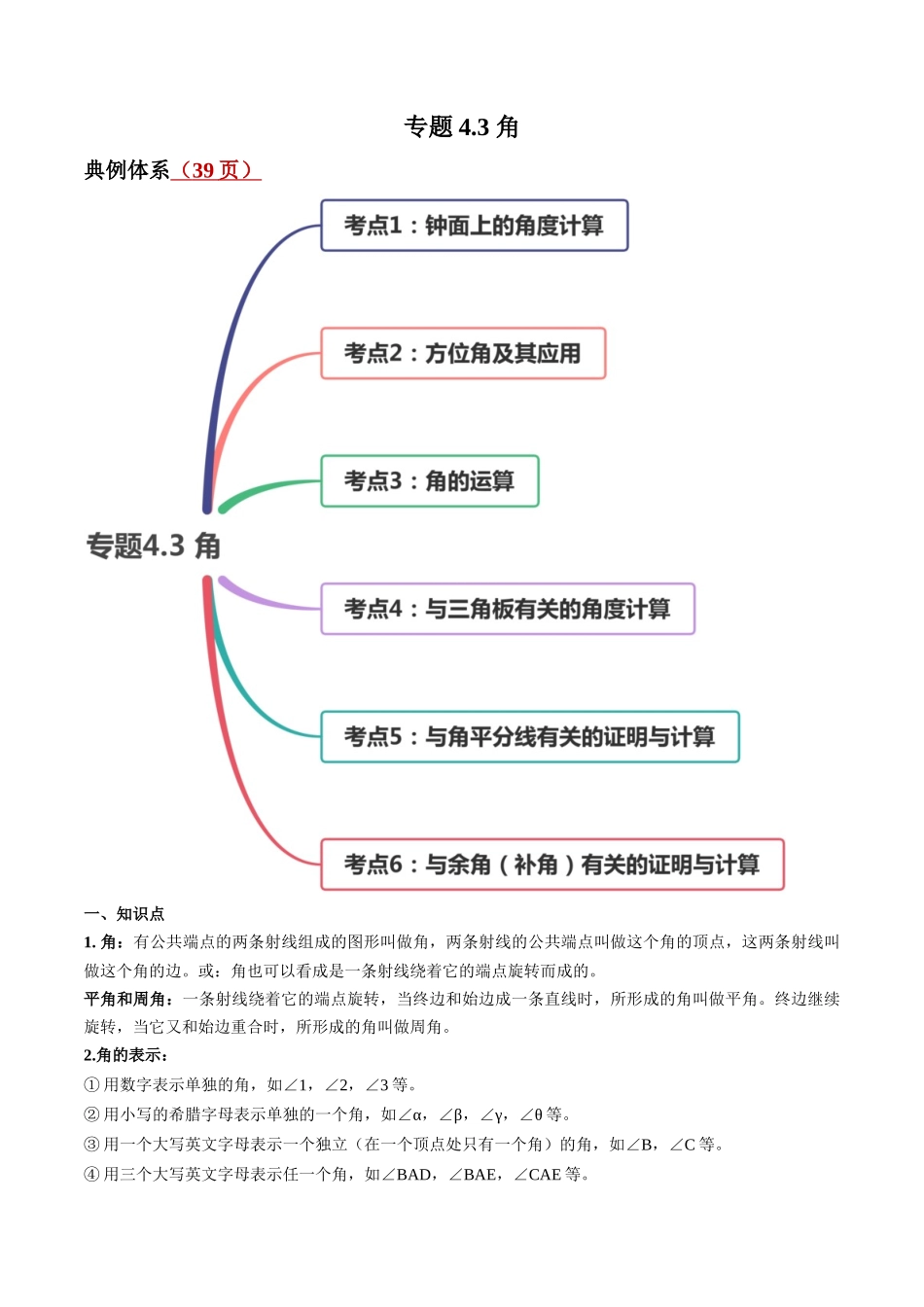
专题4.3角典例体系(39页)一、知识点1.角:有公共端点的两条射线组成的图形叫做角,两条射线的公共端点叫做这个角的顶点,这两条射线叫做这个角的边。或:角也可以看成是一条射线绕着它的端点旋转而成的。平角和周角:一条射线绕着它的端点旋转,当终边和始边成一条直线时,所形成的角叫做平角。终边继续旋转,当它又和始边重合时,所形成的角叫做周角。2.角的表示:①用数字表示单独的角,如∠1,∠2,∠3等。②用小写的希腊字母表示单独的一个角,如∠α,∠β,∠γ,∠θ等。③用一个大写英文字母表示一个独立(在一个顶点处只有一个角)的角,如∠B,∠C等。④用三个大写英文字母表示任一个角,如∠BAD,∠BAE,∠CAE等。注意:用三个大写英文字母表示角时,一定要把顶点字母写在中间,边上的字母写在两侧。3.用一副三角板,可以画出15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,165°4.角的度量角的度量有如下规定:把一个平角180等分,每一份就是1度的角,单位是度,用“°”表示,1度记作“1°”,n度记作“n°”。把1°的角60等分,每一份叫做1分的角,1分记作“1’”。把1’的角60等分,每一份叫做1秒的角,1秒记作“1””。1°=60’,1’=60”5.角的性质(1)角的大小与边的长短无关,只与构成角的两条射线的幅度大小有关。(2)角的大小可以度量,可以比较(3)角可以参与运算。6.角的平分线从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线。7.余角和补角①如果两个角的和是一个直角,这两个角叫做互为余角,简称互余,其中一个角是另一个角的余角。用数学语言表示为如果∠α+∠β=90°,那么∠α与∠β互余;反过来,如果∠α与∠β互余,那么∠α+∠β=90°②如果两个角的和是一个平角,这两个角叫做互为补角,简称互补,其中一个角是另一个角的补角。用数学语言表示为如果∠α+∠β=180°,那么∠α与∠β互补;反过来如果∠α与∠β互补,那么∠α+∠β=180°③同角(或等角)的余角相等;同角(或等角)的补角相等。二、考点点拨与训练考点1:钟面上的角度计算典例:(2020·福建宁化·初一期末)上午时,钟表的时针与分针的夹角为()A.B.C.D.【答案】B【解析】解: 钟表中一圈有12个大格∴1个大格的对应的角度为360°÷12=30° 时,时针与分针间有2个大格∴此时钟表的时针与分针的夹角为30°×2=60°故选B.方法或规律点拨此题考察的是求钟表的分针与时针的...