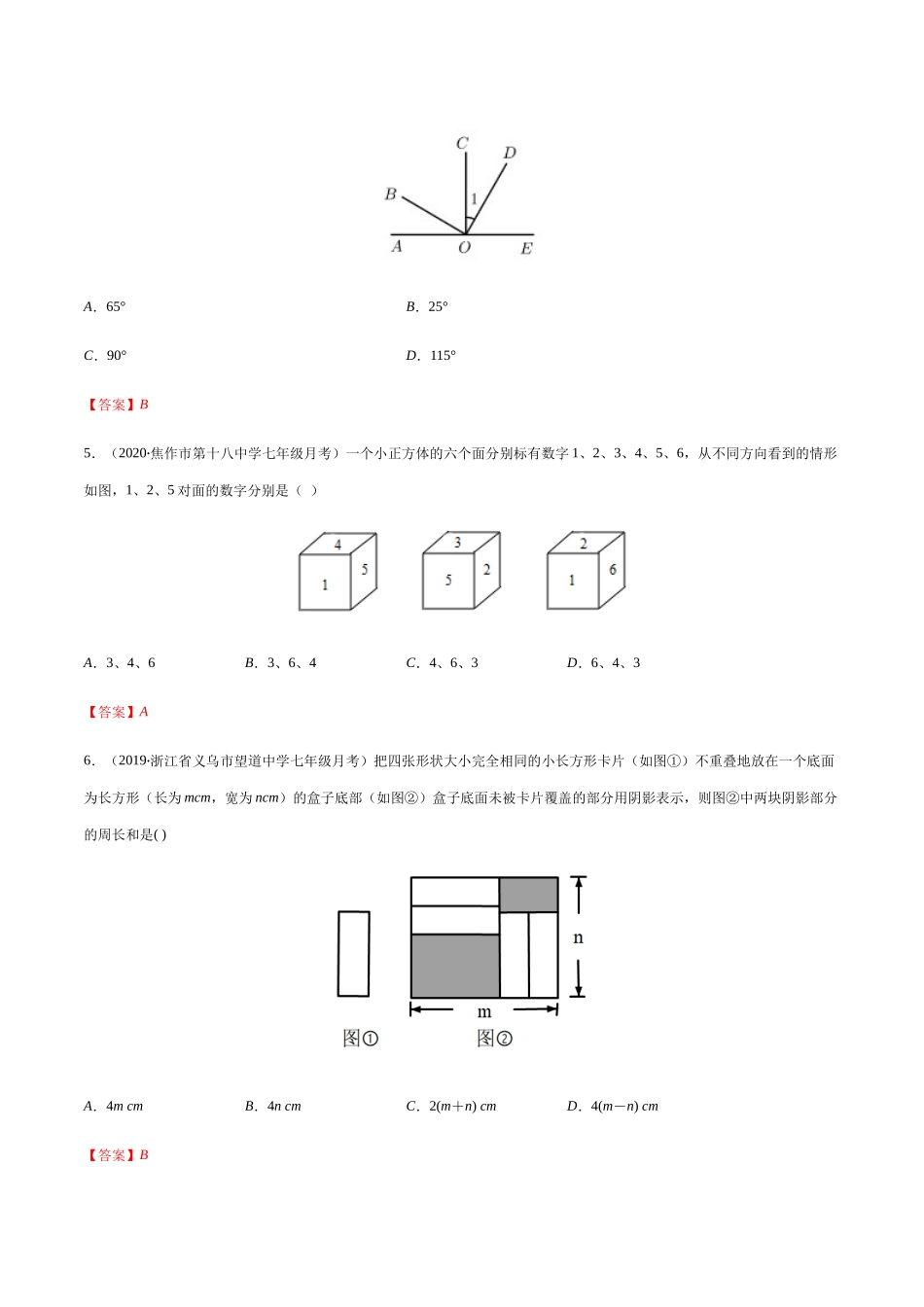
2020-2021学年七年级数学上册期末综合复习专题提优训练(人教版)期末检测卷02一、选择题(本题共计6小题,每题3分,共计18分)1.(2020·重庆市大坪中学校七年级月考)如果向左走3米记作+3米,那么向右走了5米可以记作()A.+3米B.-3米C.+5米D.-5米【答案】D2.(2020·安徽涡阳县·雪枫中学七年级期中)下列运算正确的是()A.B.C.D.【答案】D3.(2019·浙江杭州市·树兰中学七年级期中),,是实数,()A.如果,那么B.如果,那么C.如果,那么D.如果,那么【答案】B4.(2020·珠海市紫荆中学七年级期中)如图,点在直线上,平分,是直角.若∠1=25°,那么的度数是().A.65°B.25°C.90°D.115°【答案】B5.(2020·焦作市第十八中学七年级月考)一个小正方体的六个面分别标有数字1、2、3、4、5、6,从不同方向看到的情形如图,1、2、5对面的数字分别是()A.3、4、6B.3、6、4C.4、6、3D.6、4、3【答案】A6.(2019·浙江省义乌市望道中学七年级月考)把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为mcm,宽为ncm)的盒子底部(如图②)盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是()A.4mcmB.4ncmC.2(m+n)cmD.4(m-n)cm【答案】B二、填空题(本题共计6小题,每题3分,共计18分)7.(2020·广西贵港市·中考真题)计算:_______________.【答案】-48.(2020·渠县崇德实验学校七年级月考)将弯曲的河道改直,可以缩短航程,其中的道理是__________.【答案】两点之间,线段最短9.(2020·江西南昌市·七年级期中)江西省团省委近目在全省学校团组织和少先队组织集中开展了“向国旗敬礼——青春致敬祖国”主题团队日活动.据统计,截至9月30日,全省共计26.35万名团员青年、少先队员参加主题团队日活动将数据26.35万用科学记数法表示为_________.【答案】2.635×10510.(2020·弥勒县朋普中学)有一个专门生产茶杯的车间,一个工人每小时平均可以加工杯身12个,或者加工杯盖15个,车间一共有90个人,若安排x人加工杯身,能使生产的杯身与杯盖刚好配套,则可列方程:______.【答案】11.(2020·四川成都市·双楠实验学校七年级期中)已知时,代数式的值是2,当时,代数式的值等于______.【答案】112.(2019·安徽瑶海区·七年级月考)如果A、B、C三点在同一直线上,且线段AB=8cm,BC=6cm,若M、N分别为AB、BC的中点,那么M、N两点之间的...