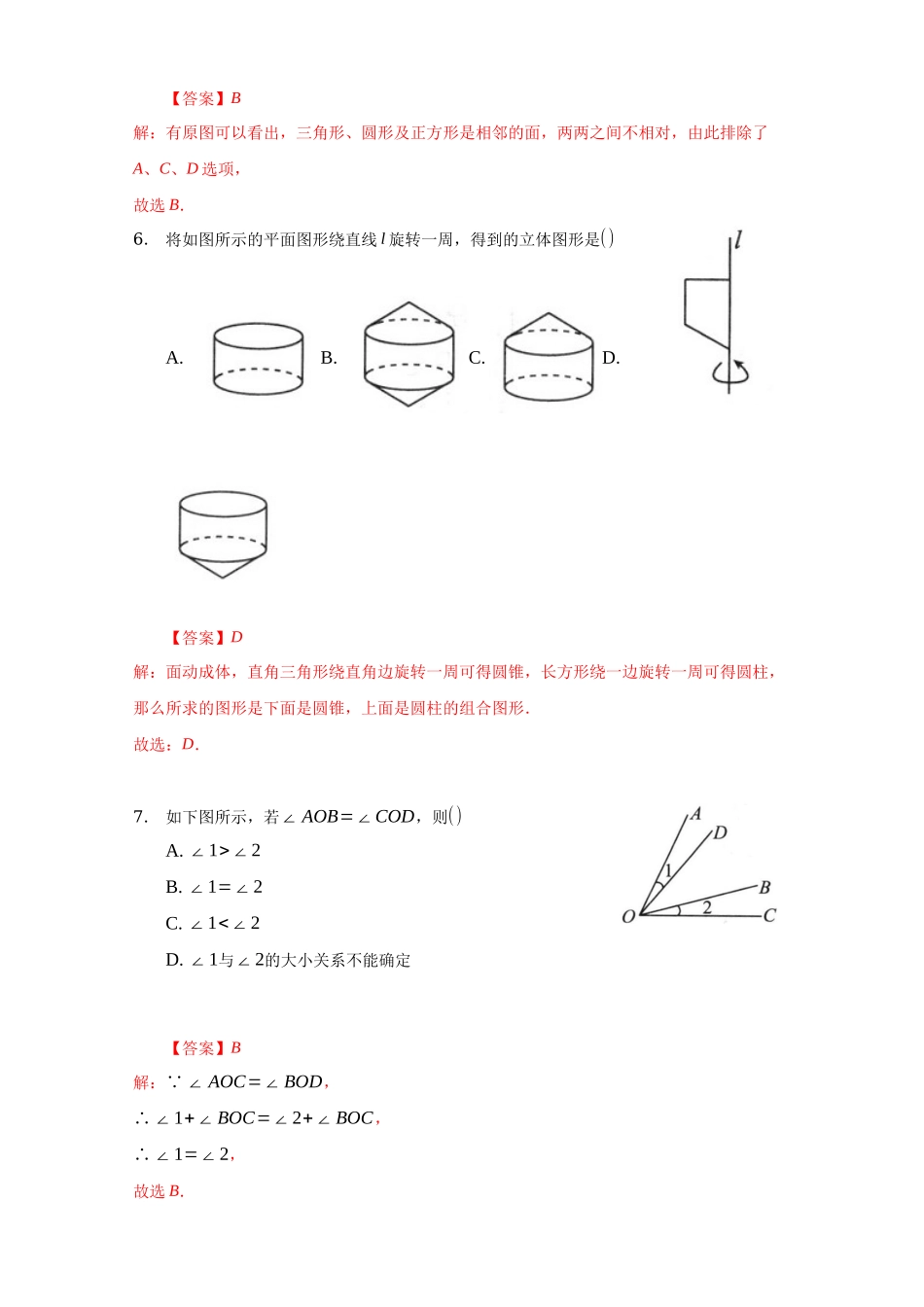
第四章几何图形初步(达标卷)解析一、选择题1.下列说法中正确的是()A.两点之间,直线最短B.画出A,B两点的距离C.连接点A与点B的线段,叫A,B两点的距离D.两点的距离是一个数,不是指线段本身【答案】D解:A.应为两点之间线段最短,故本选项错误;B.画出的应是两点间的图形,而不是距离,故本选项错误;C.应为连接两点间的线段的长度叫两点的距离,故本选项错误;D.两点之间的距离是一个数,不是指线段本身,故本选项正确.故选D.2.对于直线AB,线段CD,射线EF,其中能相交的是下图中的()A.B.C.D.【答案】B解:A、直线AB与线段CD不能相交,故本选项错误;B、直线AB与射线EF能够相交,故本选项正确;C、射线EF与线段CD不能相交,故本选项错误;D、直线AB与射线EF不能相交,故本选项错误.故选B.3.如图所示的四个图中,能用∠1,∠AOB,∠O三种方法表示同一个角的是()A.B.C.D.【答案】D第2页,共3页解:A.图中的∠AOB不能用∠O表示,故本选项错误;B.图中的∠1和∠AOB不能用∠O表示,故本选项错误;C.图中的∠AOB不能用∠O表示,故本选项错误;D.图中∠1、∠AOB、∠O表示同一个角,故本选项正确.故选D.4.如图,C是线段AB的中点,D是线段CB的中点,下列说法错误的是()A.CD=AC−BDB.AD=AB−BDC.AC+BD=BC+CDD.CD=12AB【答案】D解:由C是线段AB的中点,D是线段CB的中点,得AC=CB,CD=DB.A、CD=CB−BD=AC−BD,故A正确;B、AD=AB−BD,故B正确;C、AC+BD=BC+CD,故C正确;D、CD=12BC=14AB,故D错误.故选D.5.下图的四个图形中,经过折叠能围成选项所示的立体图形的是()A.B.C.D.【答案】B解:有原图可以看出,三角形、圆形及正方形是相邻的面,两两之间不相对,由此排除了A、C、D选项,故选B.6.将如图所示的平面图形绕直线l旋转一周,得到的立体图形是()A.B.C.D.【答案】D解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,那么所求的图形是下面是圆锥,上面是圆柱的组合图形.故选:D.7.如下图所示,若∠AOB=∠COD,则()A.∠1>∠2B.∠1=∠2C.∠1<∠2D.∠1与∠2的大小关系不能确定【答案】B解: ∠AOC=∠BOD,∴∠1+∠BOC=∠2+∠BOC,∴∠1=∠2,故选B.第4页,共3页8.一个锐角的余角比它的补角()A.相等B.小90∘C.大90∘D.不能确定大小【答案】B解:设这个锐角是α,则它的余角是90°−α,它的补角是180°−α,所以一个锐角的余角比它的补角小180°−α−(90°−α)=90°.故选B.9.点A,B,C,D,E的位置如图...