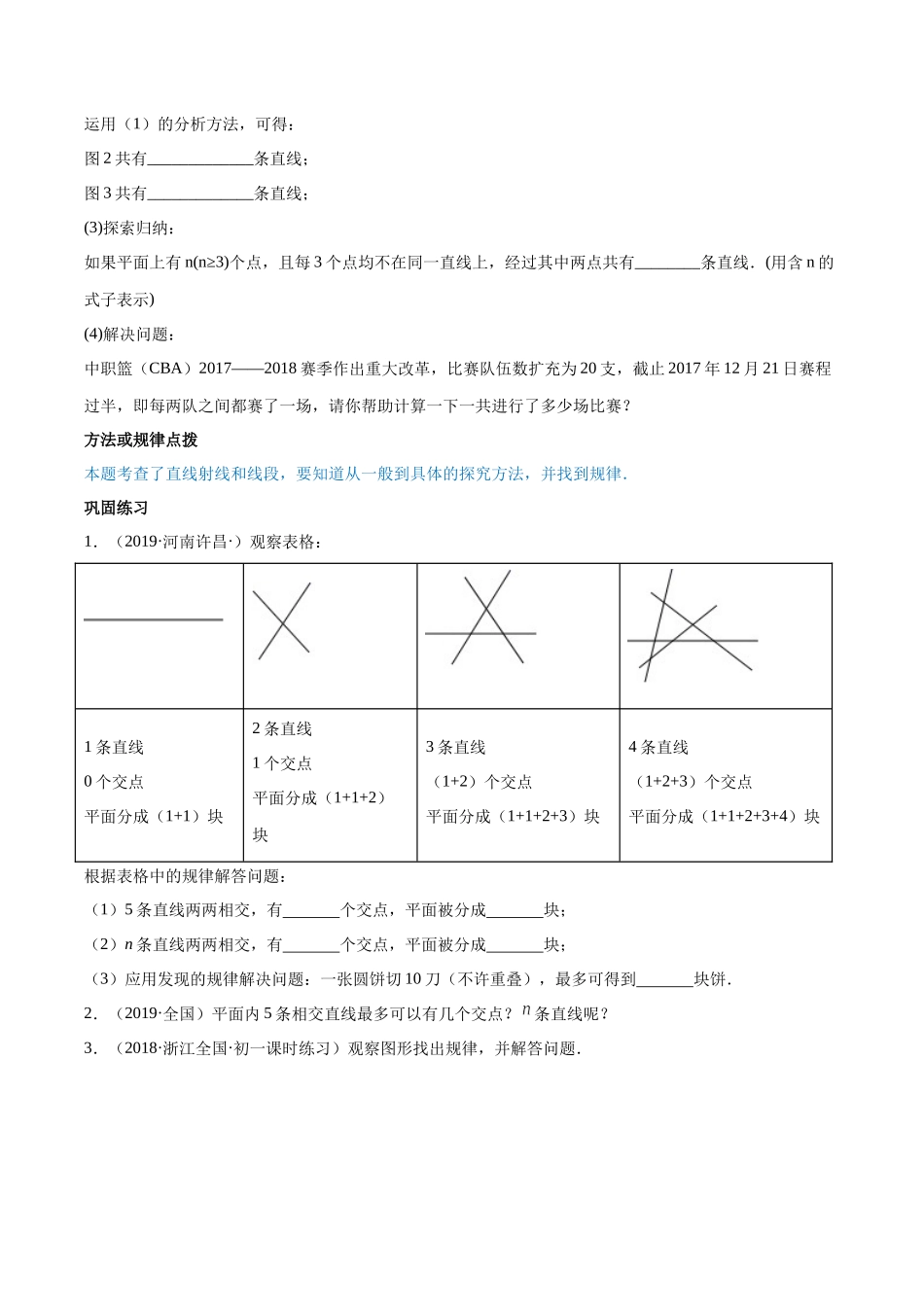
第04章重点突破训练:与线段和角有关的证明与计算考点体系考点1:与线段有关的计数问题典例:(2018·内蒙古宁城·初一期末)探究归纳题:(1)试验分析:如图1,经过A点与B、C两点分别作直线,可以作____________条;同样,经过B点与A、C两点分别作直线,可以作______________条;经过C点与A、B两点分别作直线,可以作___________条.通过以上分析和总结,图1共有___________条直线.(2)拓展延伸:运用(1)的分析方法,可得:图2共有_____________条直线;图3共有_____________条直线;(3)探索归纳:如果平面上有n(n≥3)个点,且每3个点均不在同一直线上,经过其中两点共有________条直线.(用含n的式子表示)(4)解决问题:中职篮(CBA)2017——2018赛季作出重大改革,比赛队伍数扩充为20支,截止2017年12月21日赛程过半,即每两队之间都赛了一场,请你帮助计算一下一共进行了多少场比赛?方法或规律点拨本题考查了直线射线和线段,要知道从一般到具体的探究方法,并找到规律.巩固练习1.(2019·河南许昌·)观察表格:1条直线0个交点平面分成(1+1)块2条直线1个交点平面分成(1+1+2)块3条直线(1+2)个交点平面分成(1+1+2+3)块4条直线(1+2+3)个交点平面分成(1+1+2+3+4)块根据表格中的规律解答问题:(1)5条直线两两相交,有个交点,平面被分成块;(2)n条直线两两相交,有个交点,平面被分成块;(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到块饼.2.(2019·全国)平面内5条相交直线最多可以有几个交点?条直线呢?3.(2018·浙江全国·初一课时练习)观察图形找出规律,并解答问题.(1)5条直线相交,最多有_____个交点,平面最多被分成_____块;(2)n条直线相交,最多有__________个交点,平面最多被分成____________块.4.(2019·全国初一)往返于A、B两地的客车,途中要停靠C、D两个车站,如图所示.则需要设定几种不同的票价?需要准备多少种车票?5.(2019·全国初一课时练习)(1)观察思考:如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;(2)模型构建:如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;(3)拓展应用:8位同学参加班上组织的象棋比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),那么一共要进行多少场比赛?请将这个问题转化为上述模型,并直接应用上述模型的结论解决问...