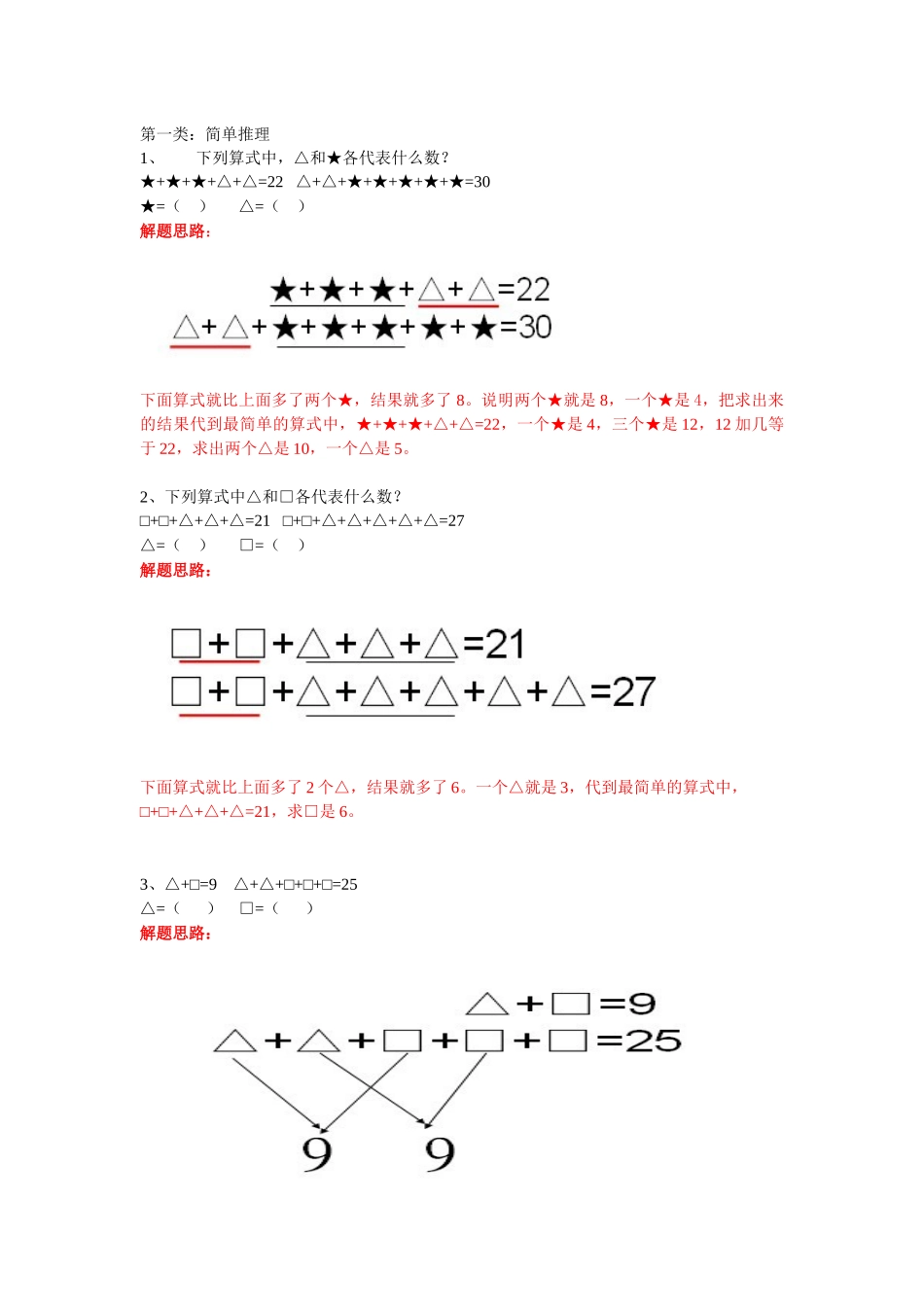
第一类:简单推理1、下列算式中,△和★各代表什么数?++++=22++++++=30★★★△△△△★★★★★=★()△=()解题思路:下面算式就比上面多了两个★,结果就多了8。说明两个★就是8,一个★是4,把求出来的结果代到最简单的算式中,★++++=22★★△△,一个★是4,三个★是12,12加几等于22,求出两个△是10,一个△是5。2、下列算式中△和□各代表什么数?□+□+++=21□+□+++++=27△△△△△△△△=△()□=()解题思路:下面算式就比上面多了2个△,结果就多了6。一个△就是3,代到最简单的算式中,□+□+++=21△△△,求□是6。3、△+□=9++□+□+□=25△△=△()□=()解题思路:一个△和一个□加起来是9,代到第2个算式中,求出□=7,再代入第一个算式△=24、□+□+=16□++=14△△△□=()△=()解题思路:上面算式和下面算式就有一个不一样,一个是□一个是△,结果多了2。说明一个□比△2,□=+2△代入到□++=14△△,△+2++=14△△。求出△=4,□=+2△,□=6。5、○+★+★=10○+★+○=8○=()★=()解题思路:一个★比一个○多2,★=○+2代入○+★+○=8,○+○+2+○=8,○=2,★=4.6、△+○=7++○=10△△○-=△()○×=△()解题思路:第二个算式就比第一个算式多一个△,结果就多3,所以△=3,○=4。1有三个女孩分别是小巧、小亚和小美,她们分别穿着花裙子、白裙子和红裙子.现在知道小巧不喜欢穿红的,小美既没有穿红的裙子,也没有穿花的裙子,她们三人各自穿的是哪条裙子?2.盘子里有香蕉、苹果和橘子三种水果小胖说:“每人只吃一种水果。”小丁丁说:“我既不吃苹果也不吃橘子,”小刚说:“我不吃橘子,”他们三人分别吃什么水果?3.小东、小西、小南、小北和小天五人之间进行乒乓球单打比赛,规定每两人之间比赛一场现在小东比赛了4场,小西比赛了2场,小南比赛了1场,小北比赛了3场,那么小天已经比赛了几场?4.如图13-2,4个小正方体排成排,每个正方体的6个面上分别写着1~6这6个数字,并且任意两个相对的面上所写的数字之和都等于7,紧贴着的两个面上的数字之和都等于8.问:打“?”的一组对面上所写的两个数字各是多少?5.要给四个商品编号,已给3个商品编了号:354.157、164.已知这四个商品的编号中,每一个数位上的数字恰好在同一数位上出现两次,问:第四个商品的编号是多少?6.检验员要对27件产品进行检验,合格品重量相同,可其中混杂了一件次品,次品的重量比合格品轻你能不能用天平3次将次品称出来?7.已知10个李子的重量...