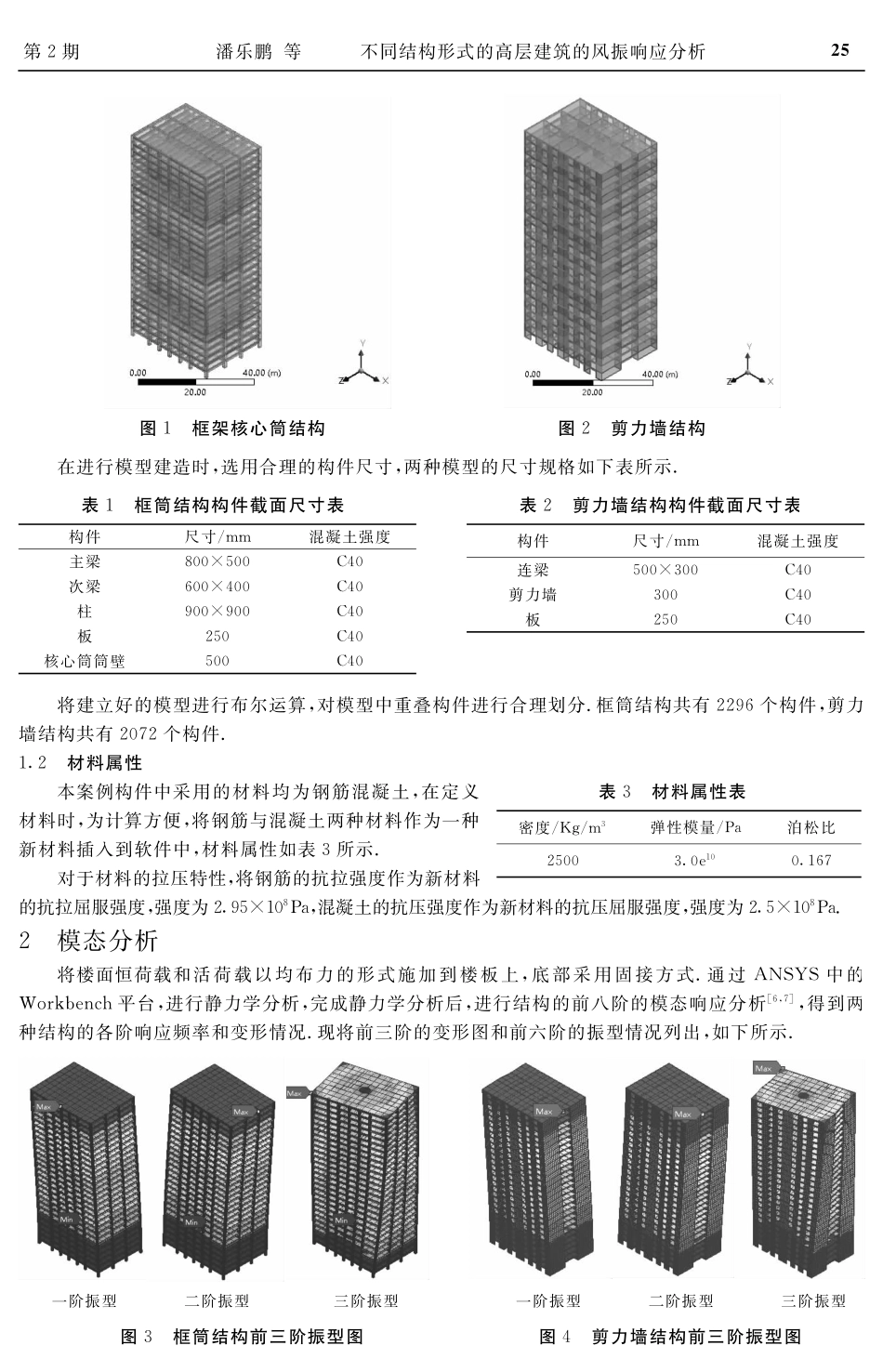
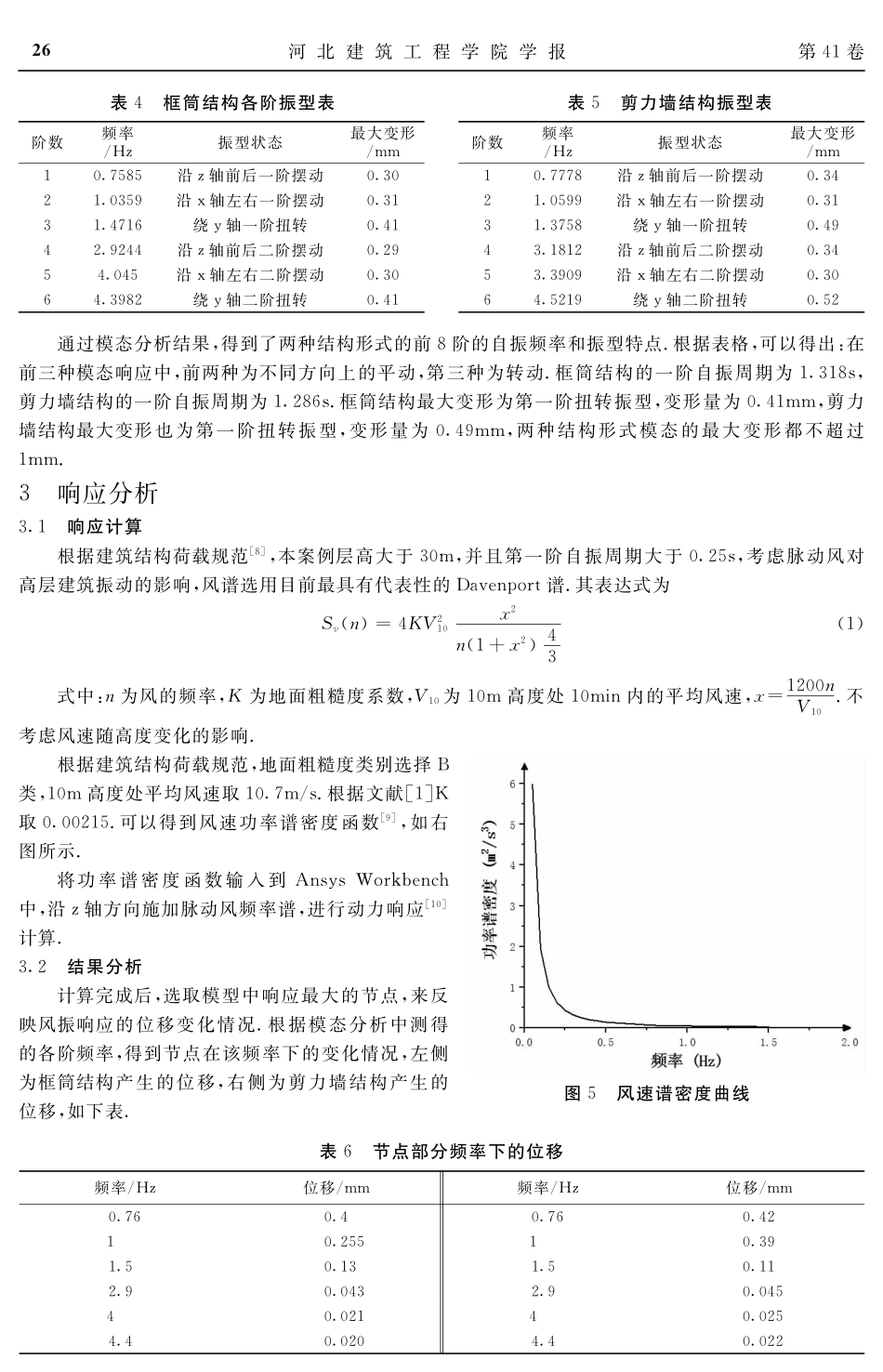
欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟欟收稿日期:20220726基金项目:2023年河北省高等学校科学技术研究项目(ZC2023028);2022年张家口市重点研发计划项目(2221007A);2021年河北省高等学校科学技术研究青年基金项目(QN2021218)作者简介:潘乐鹏(1995),男,在读硕士研究生,研究方向:岩土方向、工程结构方向。通讯作者:郁雯(1981),女,副教授,硕士生导师,主要研究方向为工程结构健康检测。犱狅犻:10.3969/j.issn.10084185.2023.02.004不同结构形式的高层建筑的风振响应分析潘乐鹏1,2张文祥1,2任淑萍1,2胡子良1,2郁雯1,2(1.河北建筑工程学院,河北张家口075000;2.河北省土木工程诊断、改造与抗灾重点实验室,河北张家口075000)摘要:为了探究高层建筑的风振响应的问题,选用高层建筑中最常用的框架核心筒与剪力墙两种结构形式。在同样的条件下,运用ANSYS软件,进行两种结构的静力学分析、模态分析和风振响应分析。经过数值计算,得到两种结构的自振频率和变形特征;根据模态分析的结果,选用脉动风谱的Davenport谱,得到两种结构的最大位移和最大加速度。经过对比,得出:框架核心筒结构的抗风性能要优于剪力墙结构。关键词:高层建筑;模态分析;风振响应;风速谱中图分类号:犜犝245文献标识码:犃0引言现如今,城市用地随着人口的不断增多正变得越来越紧张,越来越多的建筑向着高层甚至超高层方向发展,像风这类的水平荷载对建筑的影响也越来越大.目前,许多学者对高层建筑的风振响应问题进行了研究,风振响应是在脉动风作用下产生的,王修琼教授对脉动风谱中的Davenport谱系数K与地面粗糙度关系进行了研究[1],在计算高层建筑风振响应时,对风谱的使用进行了优化,提高了高层建筑中风振响应计算时数据的准确性;在进行风振响应计算时,大多数采用软件模拟的方法,像朱洁和刘润富首先利用MATLAB软件进行风速时程响应分析,然后通过ANSYS软件进行高层建筑的风振响应计算,得到建筑物顶端的加速度时程响应,并对建筑物的舒适度进行了研究[2,3];王新锋利用ABAQUS软件进行风振响应分析,并为高层建筑剪力墙的布置提供了一些建议[4...