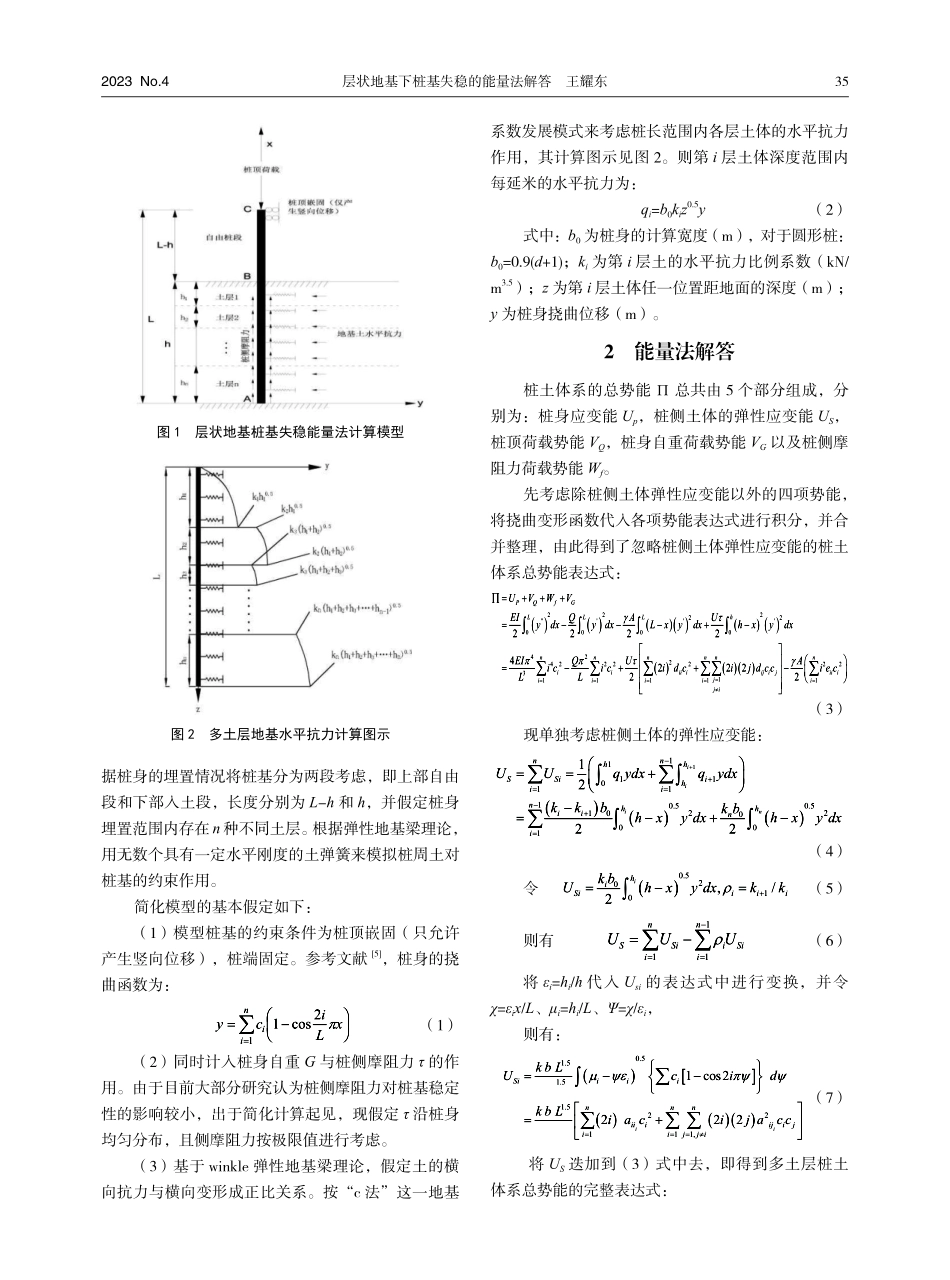
铁道勘测与设计RAILWAYSURVEYANDDESIGN2023(4)34层状地基下桩基失稳的能量法解答王耀东(中铁第四勘察设计院集团有限公司桥梁院武汉430063)【摘要】按“c法”这一地基系数模式分层考虑桩周土的水平抗力,同时计入桩身自重及侧摩阻力的作用,建立了层状地基下的桩土体系总势能方程,并采用能量法对桩基的失稳临界荷载解答进行了推导。结合某一具体算例,计算了桩基的失稳临界荷载,判断桩基是否会发生失稳破坏。结果表明:既定挠曲函数的收敛半波数为17,此时桩基的失稳临界荷载为4.57×106kN,大于桩基发生强度破坏时的极限承载力。【关键词】层状地基桩基稳定性分析能量法TheenergymethodsolutionofpilefoundationinstabilityunderlayeredsoilWANGYaodong(ChinaRailwaySIYUANSurveyandDesignGroupCo.,Ltd.,Wuhan,430063)Abstract:Accordingtothefoundationcoefficientmodelof"cmethod",thehorizontalresistanceofthesoilaroundthepileisconsideredlayerbylayer,andtheeffectsofthepilebodyweightandlateralfrictionresistancearealsotakenintoaccount.Thetotalpotentialenergyequationofthepile-soilsystemunderthelayeredfoundationisestablished,andTheenergymethodisusedtoderivethesolutiontothecriticalloadofpilefoundationinstability.Combinedwithaspecificcalculationexample,thecriticalloadofthepilefoundationinstabilityiscalculatedtodeterminewhetherthepilefoundationwillfail.Theresultsshowthattheconvergencehalf-wavenumberofthegivendeflectionfunctionis17,andthecriticalloadfortheinstabilityofthepilefoundationatthistimeis4.57×106kN,whichisgreaterthantheultimatebearingcapacitywhenthepilefoundationundergoesstrengthfailure.Keywords:layeredfoundation;pilefoundation;stabilityanalysis;energymethod0引言随着高承台桩和超长桩的广泛使用,许多学者和工程师们发现这类桩基础的破坏形式与常规的桩基础不同,多呈现为类似于弹性压杆纵向挠曲破坏的形式,因此对于桩基稳定性问题的研究越来越受到众多专家学者们的重视[1]。早在上世纪60年代,国外的专家学者们便致力于从理论分析的角度给出桩基失稳临界荷载的解答,其中比较典型的代表有:Bowles[2]提出的有限单元解、Reddy等[3]针对完全和部分入土桩提出的能量法解答及Poulos等[4]将地基土看作均质、连续、各向同性的线弹性半无限空间体而提出的弹性理论解...