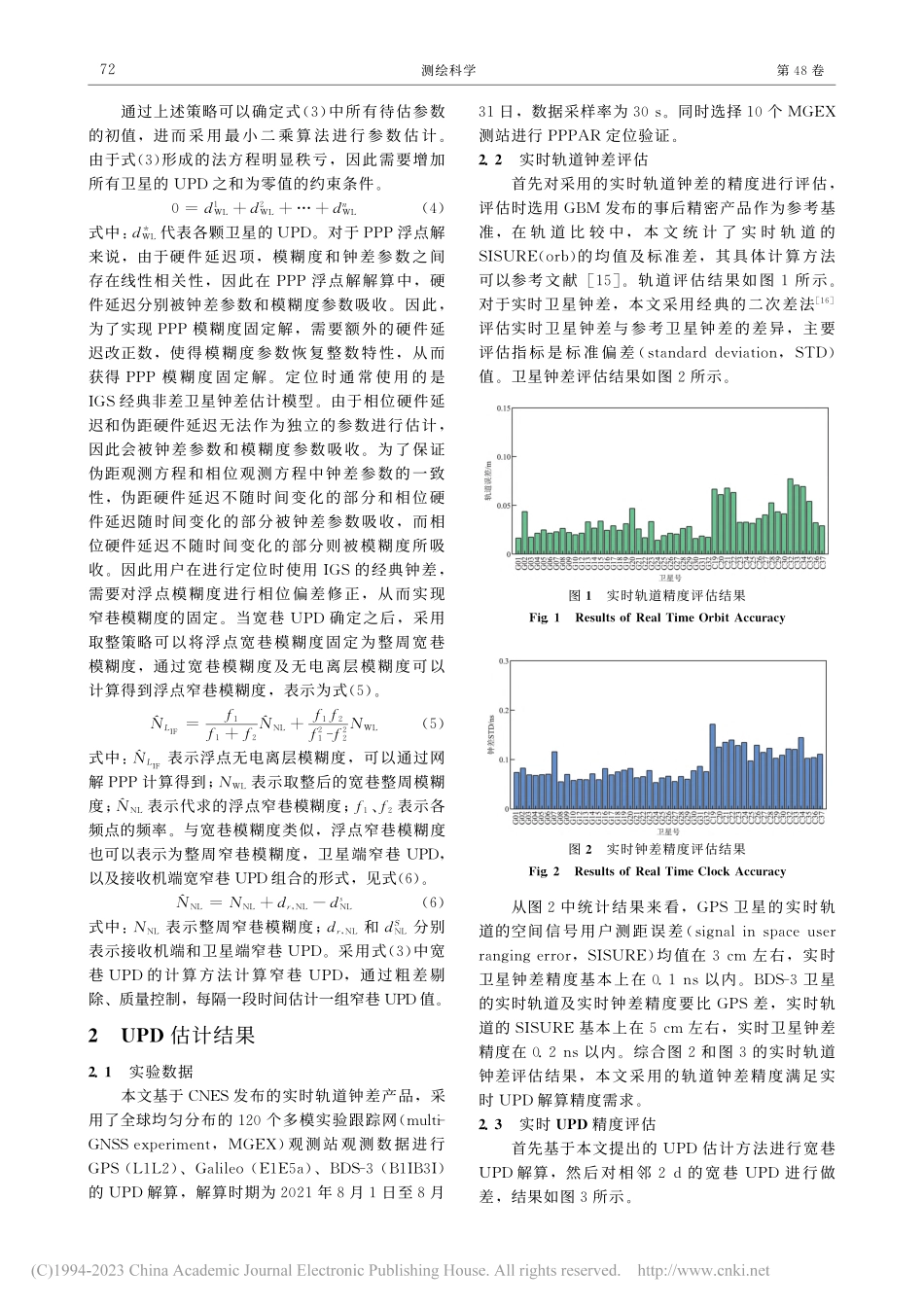
第48卷第2期2023年2月测绘科学ScienceofSurveyingandMappingVol.48No.2Feb.2023作者简介:陈刚(1985—),男,河南郑州人,讲师,硕士,主要研究方向为GNSS数据处理及应用。E-mail:chcgrtppp@163.com收稿日期:2022-06-06引文格式:陈刚.实时模式下UPD产品计算及PPPAR定位性能分析[J].测绘科学,2023,48(2):70-76.(CHENGang.Real-timeUPDproductestimationandPPPARperformanceanalysis[J].ScienceofSurveyingandMapping,2023,48(2):70-76.)DOI:10.16251/j.cnki.1009-2307.2023.02.009.实时模式下UPD产品计算及PPPAR定位性能分析陈刚(河南测绘职业学院测绘工程系,郑州450015)摘要:针对目前实时精密单点定位(PPP)收敛速度还相对较慢的问题,该文提出了一种适用于实时模式的宽巷及窄巷相位小数偏差(UPD)估计算法。采用180个全球均匀分布的多模实验跟踪网(MGEX)站,分析了基于实时轨道钟差产品进行实时UPD解算及实时精密单点定位模糊度固定(PPPAR)定位的可行性。实验结果表明,GPS和BDS-3的相邻两天宽巷UPD相减所得偏差的均值以及标准差基本上在0.025周左右,因此采用宽巷UPD预报值进行后续解算是可靠的。GPS浮点PPP和PPPAR定位结果表明,PPPAR的定位误差相较于浮点解PPP在E、N、U方向分别提升了36.4%、25.0%和22.2%,定位收敛时间也从31.9min下降到24.8min。GPS+BDS-3的PPPAR定位结果表明,定位时加入BDS-3可以缩短PPPAR的首次固定时间,最终的三维定位误差也从单GPS系统的2.55cm下降到了GPS+BDS-3的2.17cm。基于实时模式UPD解算和PPPAR定位实验结果表明,该文提出的UPD实时估计算法是可靠的,估计出的实时UPD产品应用于PPPAR可以获得较好的定位效果。关键词:实时;相位小数偏差;模糊度固定解;BDS-3【中图分类号】P228.4【文献标志码】A【文章编号】1009-2307(2023)02-0070-07Real-timeUPD...