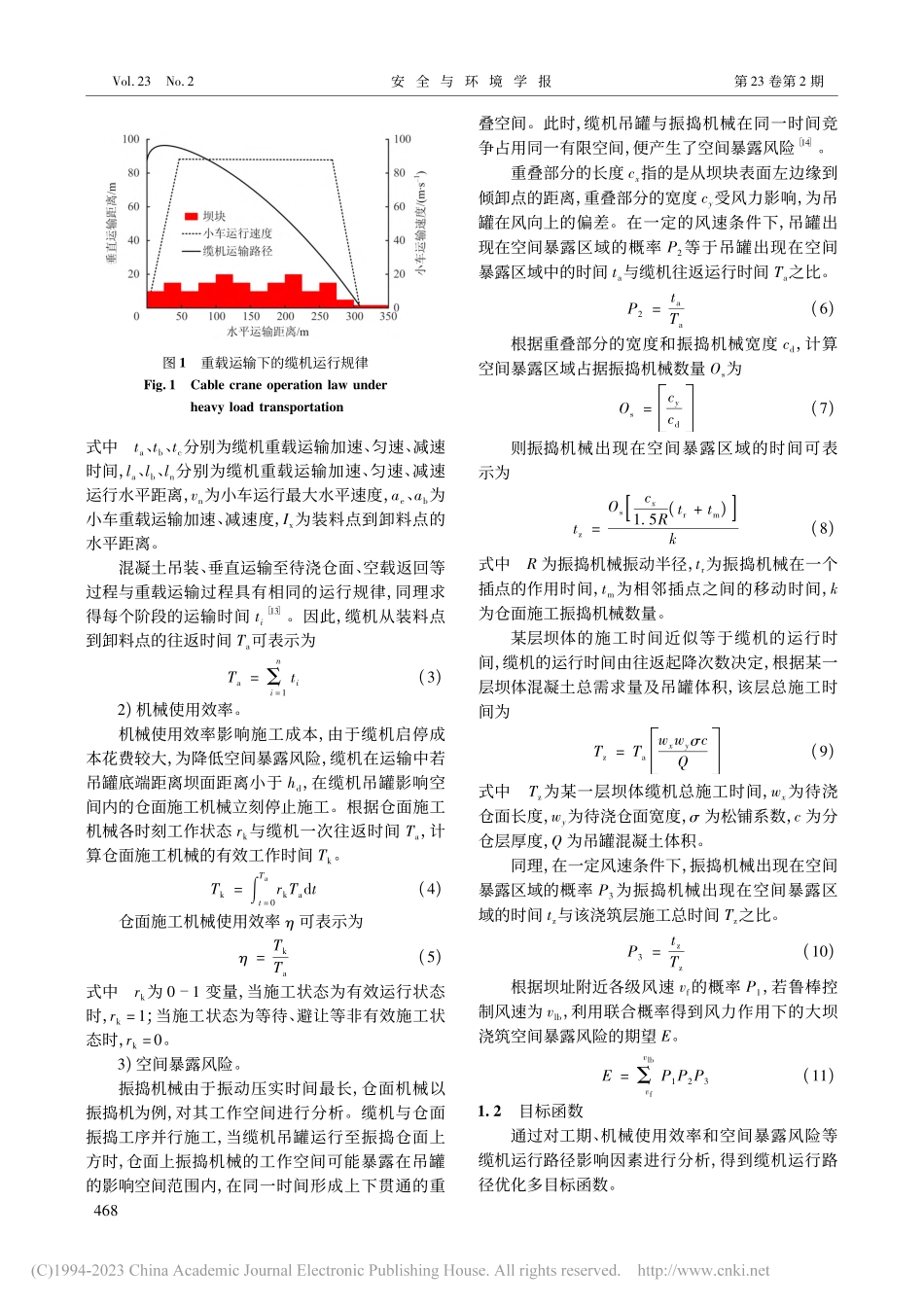
文章编号:1009-6094(2023)02-0467-07抑制风力不确定扰动的缆机运行路径鲁棒优化*陈述1,2,刘雨2,王建平1,2,陈云1(1湖北省水电工程施工与管理重点实验室(三峡大学),湖北宜昌443002;2三峡大学经济与管理学院,湖北宜昌443002)摘要:不确定性风力易导致缆机垂直运输过程中产生振荡效应,降低施工工效,甚至诱发安全事故。为抑制风力对缆机运行的不确定扰动,分析工期、机械使用效率和空间暴露风险等缆机运行路径优化目标及约束条件,运用鲁棒变换思想,将缆机运行路径规划问题抽象为多目标鲁棒优化模型,并采用交叉熵进化算法求解具有鲁棒性的帕累托前沿及缆机运行路径。案例结果表明,随鲁棒保守度增大,风力等随机性因素的影响不断增强,需要增加工期和降低机械使用效率,使空间暴露风险降低,表明所获得的帕累托前沿能够减小风力等不确定性干扰并满足工期、效率和风险等多目标需求。关键词:安全工程;鲁棒优化;缆机路径;不确定风力;空间暴露风险中图分类号:X947文献标志码:ADOI:10.13637/j.issn.1009-6094.2021.1800*收稿日期:20211015作者简介:陈述,教授,博士,从事安全管理研究,chenshu@ctgu.edu.cn;王建平(通信作者),副教授,博士,从事安全管理研究,wjp@ctgu.edu.cn。基金项目:国家自然科学基金项目(52079073)0引言缆机具有生产效率高、工作范围大等优点,在水电工程施工中应用广泛[1]。当前我国在建拟建水电工程多位于西部干热河谷地带,6级以上大风频繁,易导致缆机垂直运输过程中产生振荡效应,降低施工工效,甚至诱发安全事故[2]。因此,开展缆机运输路径多目标优化,抑制不确定性风力的扰动,对于实现项目目标及保证施工安全具有重要意义。缆机运输路径优化涉及工期、机械运行效率、安全风险等众多指标,属于多目标优化问题,国内外众多学者已开展大量研究。2017年,Wu等[3]利用全球定位系统(GlobalPositioningSystem,GPS)引导缆机运输路线,并首次建立了缆机运输路径多目标优化模型,为优化缆机运输路径奠定了基础。2020年,陈述等[4]第一次考虑风力对缆机运行的影响,结合不同风速出现的概率,采用联合概率定量计算空间冲突频率,为降低缆机运行风险奠定了基础。Wu等[5]针对桥式起重机运行系统,提出了一种时间最优轨迹规划方法,对起重机运行工期进行优化。徐建江等[67]对于传统混凝土运输过程中联动管控难和信息反馈时效低等问题,建立混凝土运输效率联动模型,提高了混凝土运输效率。吴浩等[8]对缆机运...