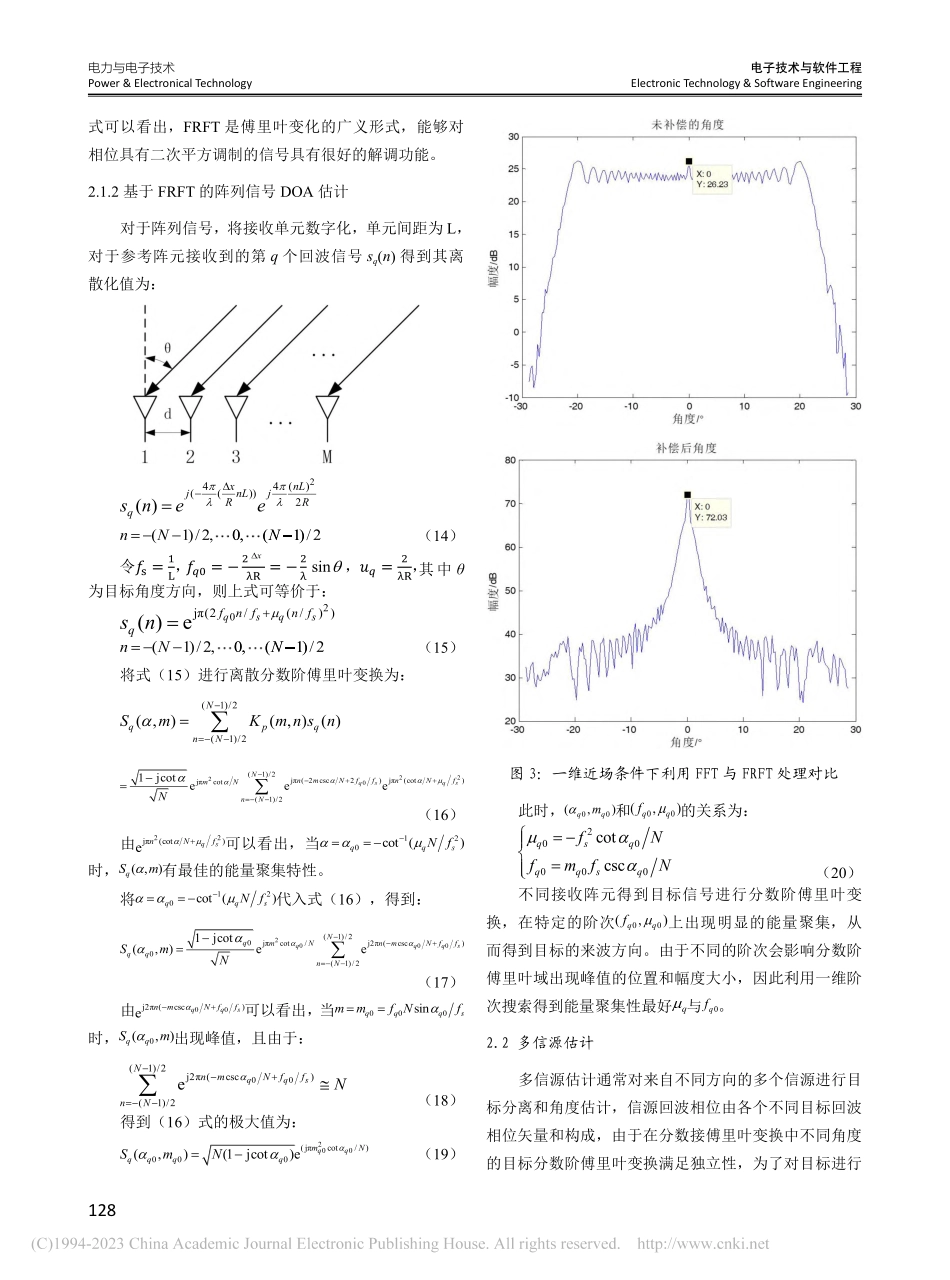
电力与电子技术Power&ElectronicalTechnology电子技术与软件工程ElectronicTechnology&SoftwareEngineering126随着智能交通的发展,无人驾驶技术日新月异,环境智能感知是实现无人驾驶的重要前提,其中车载防撞系统是环境智能感知的重要组成部分。车载防撞不仅对角度分辨率、探测距离的更高态势感知要求;而且更关注近距目标,准确定位近距目标,进行自动驾驶的辅助决策。当目标落入天线近场后,传统的菲涅尔区域的平面波的假设不再成立,波前的固有弯曲将不能忽略,因此需要研究近场条件下的多信源角度估计问题。针对近场DOA估计,学者提出了二维近场MUSIC算法[1,2],ESPRIT高阶近场估计算法[3],以及在MUSIC和ESPRIT算法基础上改进的算法[4,5],但这些算法在低信噪比下,出现估计的精度和分辨率的严重下降。时频分析是一种在地信噪比条件下有效检测目标的方法,最常用的方法[6-8]是将Wigner-Ville分布(WVD)与阵列信号相结合,但在多信号情况下WVD存在的交叉项严重影响了信号的选取和DOA估计精度。分数阶傅里叶变换(FRFT)是一种线性变换,不存在交叉项干扰,而且FRFT对具有二次项的信号有极好的聚集性,在分数阶傅里叶域集中在一点,不存在二次型时频分布的选点问题,能很方便地分离近场信号并可同时估计信号的参数。1近场观测模型假设r为信源距离阵列相位中心的距离,θ和δ分别为信源相对于阵列中心方位角和俯仰角,近场波面为球面,波动方程可以写为如下形式:(1)式中,c为电磁波速度,假设在各向同性的介质中信号s不随θ和δ变化,因此可以记为s(r,t),其中t为传输时间,则上式可以改写为:(2)上式的解为:(3)其中,A为信号源的幅度,A/r为信号传播至r处的信号幅度,fc为信号载波频率,λ为信号波长,从上式可以看出,阵元接收的信号相位和幅度均受传播距离r的影响。1.1一维天线模型如图1所示,以天线的几何中心为原点,以天线右向为x轴,垂直天线方向为y轴,建立一维坐标系,天线的总长度为L,点目标P位于y轴方向,垂直距离为R,一种基于FRFT的多信源近场DOA估计李飞呼斌(西安电子工程研究所陕西省西安市710100)摘要:本文提出了一种利用分数阶傅里叶变换进行近场多信源角度估计的方法。针对无人驾驶环境感知近场条件下目标的一维和两维信号模型,利用分数阶傅里叶变换计算二次项系数,进而得到目标来波方向角度估计;采用CLEAN方式进行信号逐一分离多个不同信源。通过仿真对近场不同类型目标进行仿真,验证算法的有效性。关键词...