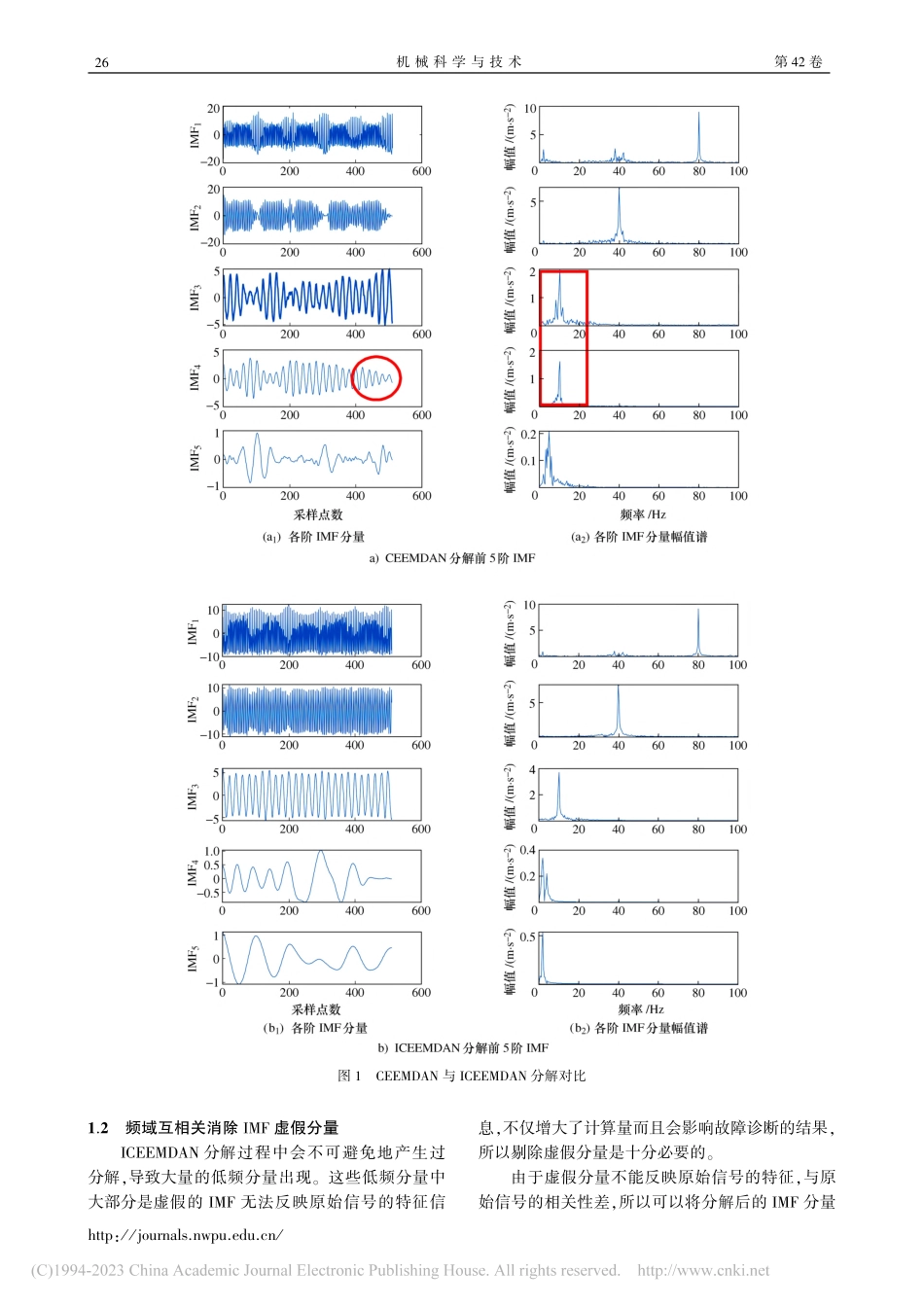
2023年第42卷1月第1期机械科学与技术MechanicalScienceandTechnologyforAerospaceEngineeringJanuaryVol.422023No.1http://journals.nwpu.edu.cn/收稿日期:20210427基金项目:国家自然科学基金项目(51175480)、山西省重点研发计划(国际合作)项目(201903D421008)及中北大学先进制造技术山西省重点实验室开放课题研究基金(XJZZ202007)作者简介:王浩楠(1997-),硕士研究生,研究方向为现场测试及机械故障诊断,1872182205@qq.com∗通信作者:崔宝珍,副教授,硕士生导师,744212889@qq.com王浩楠,崔宝珍,彭智慧,等.应用ICEEMDAN和SVM的行星齿轮箱故障诊断[J].机械科学与技术,2023,42(1):24⁃30应用ICEEMDAN和SVM的行星齿轮箱故障诊断王浩楠,崔宝珍∗,彭智慧,任川(中北大学机械工程学院,太原030051)摘要:针对行星齿轮箱复合故障准确分类问题,应用了改进自适应噪声完备集合经验模态分解(ICEEMDAN)和支持向量机(SVM)相结合的故障诊断方法。首先,将行星齿轮箱的不同故障信号分别进行ICEEMDAN分解,得到各阶内禀模态函数(IMF);其次,利用各阶IMF分量与原信号的相关性大小,剔除虚假的IMF分量;最后,以优选IMF分量的多尺度模糊熵均值作为特征向量,输入到多分类SVM中进行故障分类,分类准确率高达100%,实验结果证明了该方法的可行性。关键词:改进自适应噪声完备集合经验模态分解;频域互相关;多尺度模糊熵;支持向量机;行星齿轮箱故障中图分类号:TH132.41文献标志码:ADOI:10.13433/j.cnki.1003⁃8728.20220020文章编号:1003⁃8728(2023)01⁃0024⁃07FaultDiagnosisofPlanetaryGearboxusingICEEMDANandSVMWANGHaonan,CUIBaozhen∗,PENGZhihui,RENChuan(CollegeofMechanicalEngineering,NorthUniversityofChina,Taiyuan030051,China)Abstract:Aimingatt...