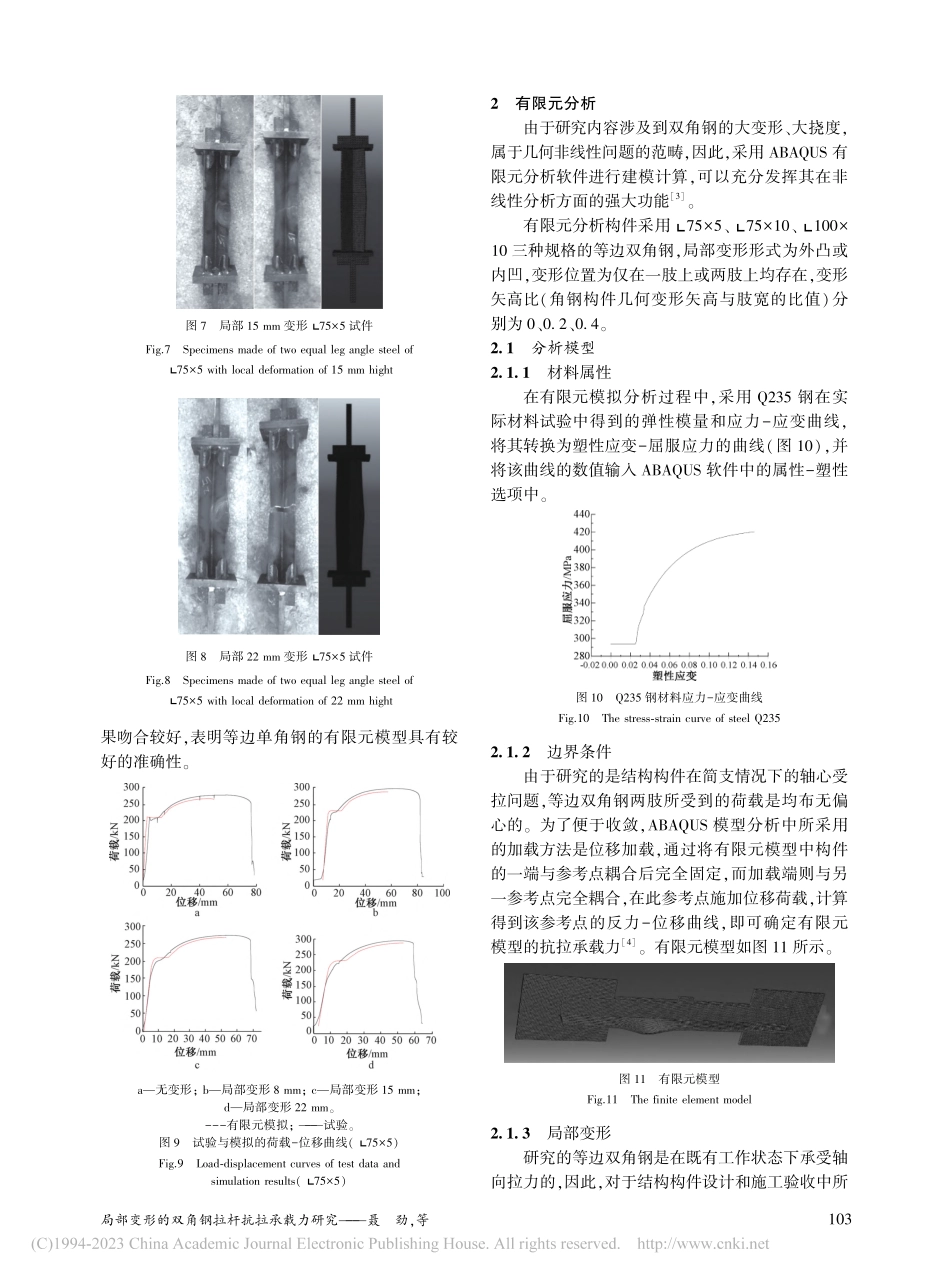
IndustrialConstructionVol.52,No.12,2022工业建筑2022年第52卷第12期101局部变形的双角钢拉杆抗拉承载力研究聂劲幸坤涛杨建平(中冶建筑研究总院有限公司,北京100088)摘要:角钢拉杆是钢结构中的常见结构构件,在实际工程中由于机械碰撞、意外事故等原因容易产生局部变形,对承载力产生不利影响。国内已有对局部变形的单角钢拉杆承载力的研究,但还缺乏对有局部凹凸变形的双角钢杆件受拉承载力的研究。通过展开局部变形角钢拉杆受拉试验并对其进行有限元模型验证,对三种不同规格的等边双角钢拉杆进行有限元模拟分析,得到了不同局部变形条件下的双角钢拉杆的抗拉承载力折减系数,可用于不同局部变形双角钢构件的抗拉承载力验算。关键词:局部变形;双角钢拉杆;抗拉承载力;有限元模拟DOI:10.13204/j.gyjzG20010903ResearchonTensileCapacityofTensileMembersofDoubleAnglewithLocalDeformationNIEJinXINGKuntaoYANGJianping(CentralResearchInstituteofBuildingandConstructionCo.,Ltd.,MCCGroup,Beijing100088,China)Abstract:Thetensilememberofanglesteelisakindofcommoncomponentforsteelstructures.Itoftenoccurslocaldeformationinpracticalprojectbecauseofmechanicalcollisionoraccidents.Therearealotofdomesticresearchonthebearingcapacityoftensilememberofsingleangle.However,whenitcomestothedoubleequal⁃anglesteelcomponentwithlocalconcave⁃convexdeformation,thereisstillalackofresearchofitsbearingcapacityinrelatedspecifications.Withtheverifiedmethodoffini...