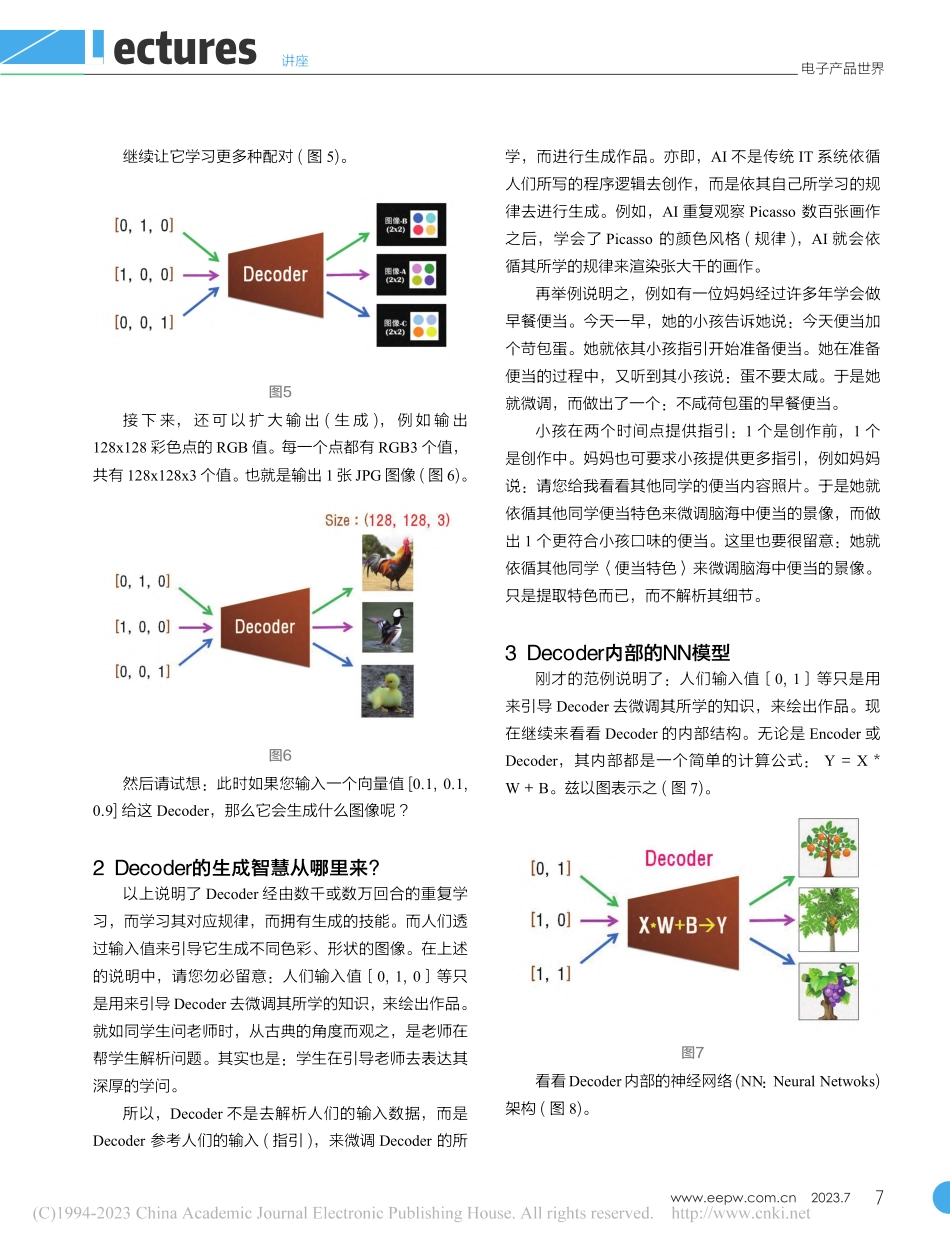
6ELECTRONICENGINEERING&PRODUCTWORLD2023.7Lectures电子产品世界$讲座从隐空间领会解码器Understandingdecodersfromeuclideanlatentspaces高焕堂0引言在上1期里,您已经领会(理解)Encoder的涵意和功能了。在本期里,就继续来领会Decoder的涵意和功能。由于这两者是息息相关的。例如在Diffusion模型里,就含有文本编码器(textencoder)、图像编码器(imagedecoder)、以及解码器(decoder)等。于是,当您已经深入理解编码器了,就能轻易继续理解另一名词:解码器(Decoder)。兹回忆上1期的说明:Encoder负责从有招的世界,萃取(过滤)&沉淀于无招世界(即AI的潜藏空间),然后由Decoder来生成千变万化的新招式。例如,上1期所举的<换脸>范例(图1)。图1来源https://arxiv.org/pdf/1909.11573.pdf您已经理解Encoder了。接下来,我们就来详细说明Decoder是如何<生成>(无中生有)呢?1Decoder如何生成?Decoder的无中生有技能是它经由机器学习(MachineLearning)过程,而获得的知识和智能;基于这学来的智慧来进行<生成>。我们先从简单的例子出发。例如,让它(即Decoder)学习:<输入1个数值--1,而输出3个数值(红色RGB的数值)--[255,0,0]。兹以图2表示。图2然后继续让学习更多。例如学习:<输入一个数值--100,而输出3个数值(绿色RGB的数值)--[0,255,0]。并且学习:<输入1个数值--200,而输出3个数值(蓝色RGB的数值)--[0,0,255]。共学习了3项智能(图3)。图3俗语说:学而时习之。让它重复学习更多回合,它就掌握上述的3项生成<规律>了。之后,只要我们输入[1]给这Decoder,它就会生成很接近于[255,0,0]的值,但不一定是[255,0,0]。同样地,只要输入[100]给这Decoder,它就会生成很接近于[0,255,0]的值,但只是近似而已。请您想一想:此时如果您输入一个值[95]给这Decoder,那么它会输出什么值呢?这只是一个起点,逐渐地扩大Decoder的能力,就能做出形形色色的图像生成了。例如,从上述范例的输出都是1个点的颜色RGB值。我们可以扩大输出(生成),例如输出4个彩色点的RGB值。每一个点都有RGB3个值,而4个点共有12个值。也就是输出1个向量,其含有12个值(图4)。图47www.eepw.com.cn2023.7电子产品世界讲座Lectures继续让它学习更多种配对(图5)。图5接下来,还可以扩大输出(生成),例如输出128x128彩色点的RGB值。每一个点都有RGB3个值,共有128x128x3个值。也就是输出1张JPG图像(图6)。图6然后请试想:此时如果您输入一个向量值[0.1,0.1,0.9]给这Decoder,那么它会生成什么图像呢?2Decoder的生成智慧从哪...