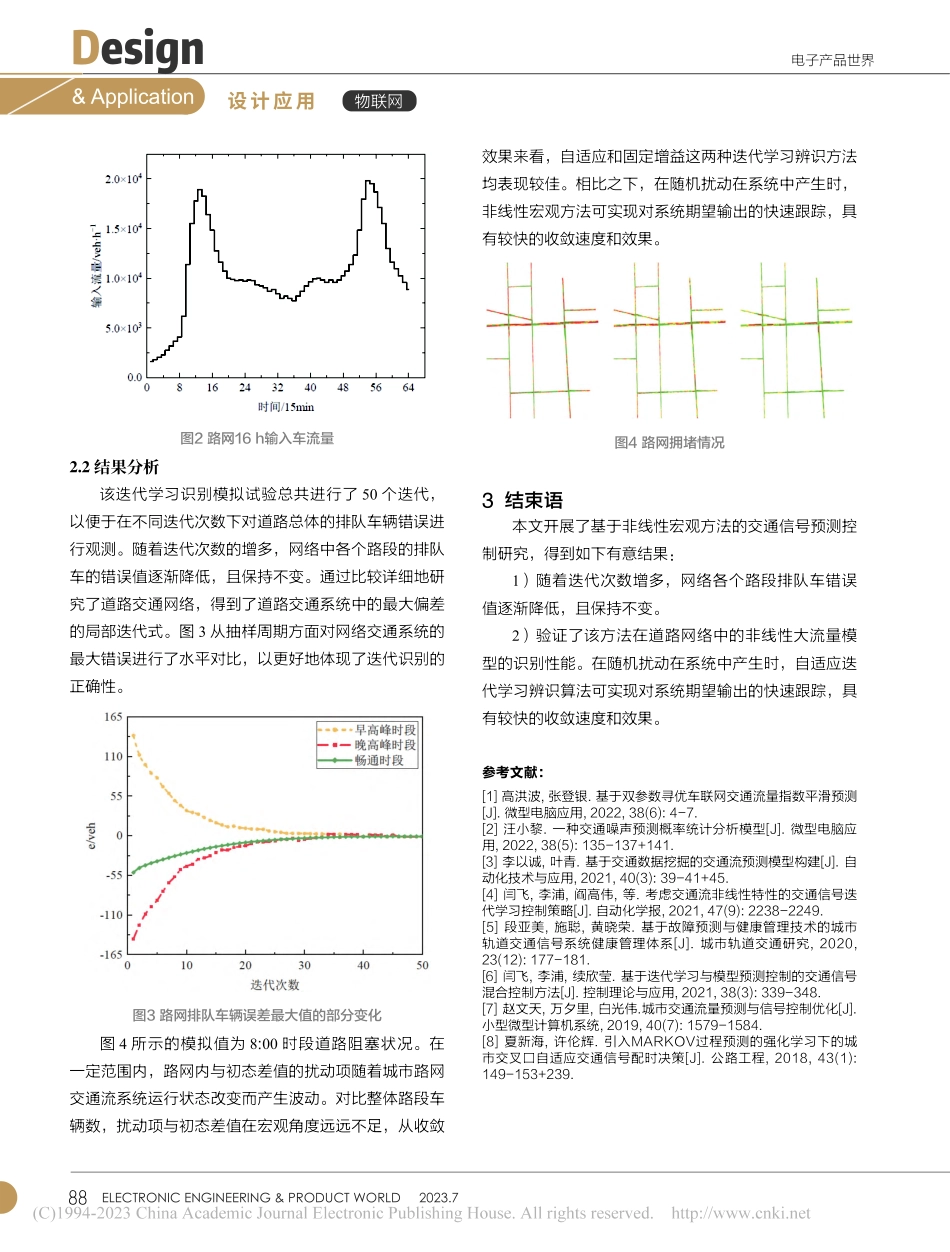
86ELECTRONICENGINEERING&PRODUCTWORLD2023.7$电子产品世界Design设计应用&Application物联网基于非线性宏观方法的交通信号预测控制分析Trafficsignalpredictivecontrolanalysisbasedonnonlinearmacroscopicmethod刘萍(北京科技大学保卫处,北京100083)摘要:为了提高城市路网设计效率,设计了一种基于非线性模型预测控制的城市路网交通流优化。采用预测控制方法,达到最大限度地提高路口的通行能力,并验证了迭代式识别在车辆流量模型的参数识别中的正确性。研究结果表明:随着迭代次数增多,网络各个路段排队车错误值逐渐降低,且保持不变。对网络交通系统的最大错误对比,以更好地体现了迭代识别正确性。虽然道路网的非线性宏观流量模型与道路模拟试验结果总体上是与道路交通流量的实际改变相一致的,验证了该方法在道路网络中的非线性大流量模型的识别性能。在随机扰动在系统中辨识算法可实现对系统期望输出的快速跟踪,具有较快收敛速度。关键词:交通流;拥堵现象;参数辨识;承载能力0引言在目前的交通系统中,关于模型预测的研究已经逐渐增多。作为管理与控制城市路网交通的基础模型,信号控制策略控制性能优劣直接取决于城市路网交通流模型质量情况[1]。通过测量的输入和输出,识别具有典型工作特性的模型参数,从而使其更好地反映生产过程中的动态过程[2]。现有的参数识别技术大都是建立在线性或缓慢变化的基础上,对于一种在一定的时间段内存在反复操作的非线性时变性,它不能很好地识别出它的参数[3]。而反复学习识别方法则可以充分发挥该系统的可重现性,以之前或以前的错误信息为纠错对象,并对其进行反复的学习,以达到识别的要求;完整地追踪参数[4]。不同于快速路、高速公路,城市路网交通流在交叉口信号控制的影响下呈现出不同的状态,段亚美等[5]专门针对城市路网交通流系统运行情况展开更深入的研究,辨识交叉口多种交通参数,得出交通流模型辨识结果与方案运行结果一致,运行状态处于交叉口处三、四相位配。闫飞等[6]则是对运行过程中,城市路网交通流系统的变化特性展开深入研究,将随机变化项引入构建的宏观交通流模型框架当中,将计算工作量降低,随机变量处理效率在宏观基本图中更快。根据迭代式识别方法特点,提出了一种新的时变性多参量的迭代式识别方法。通过一个城市道路网络的模拟试验表明,该方法能够有效地识别时变量多参数的动态系统。1交通信号预测控制研究1.1控制目标在道路系统流量饱和的条件下,道路网络的车辆通过与道路网络的...