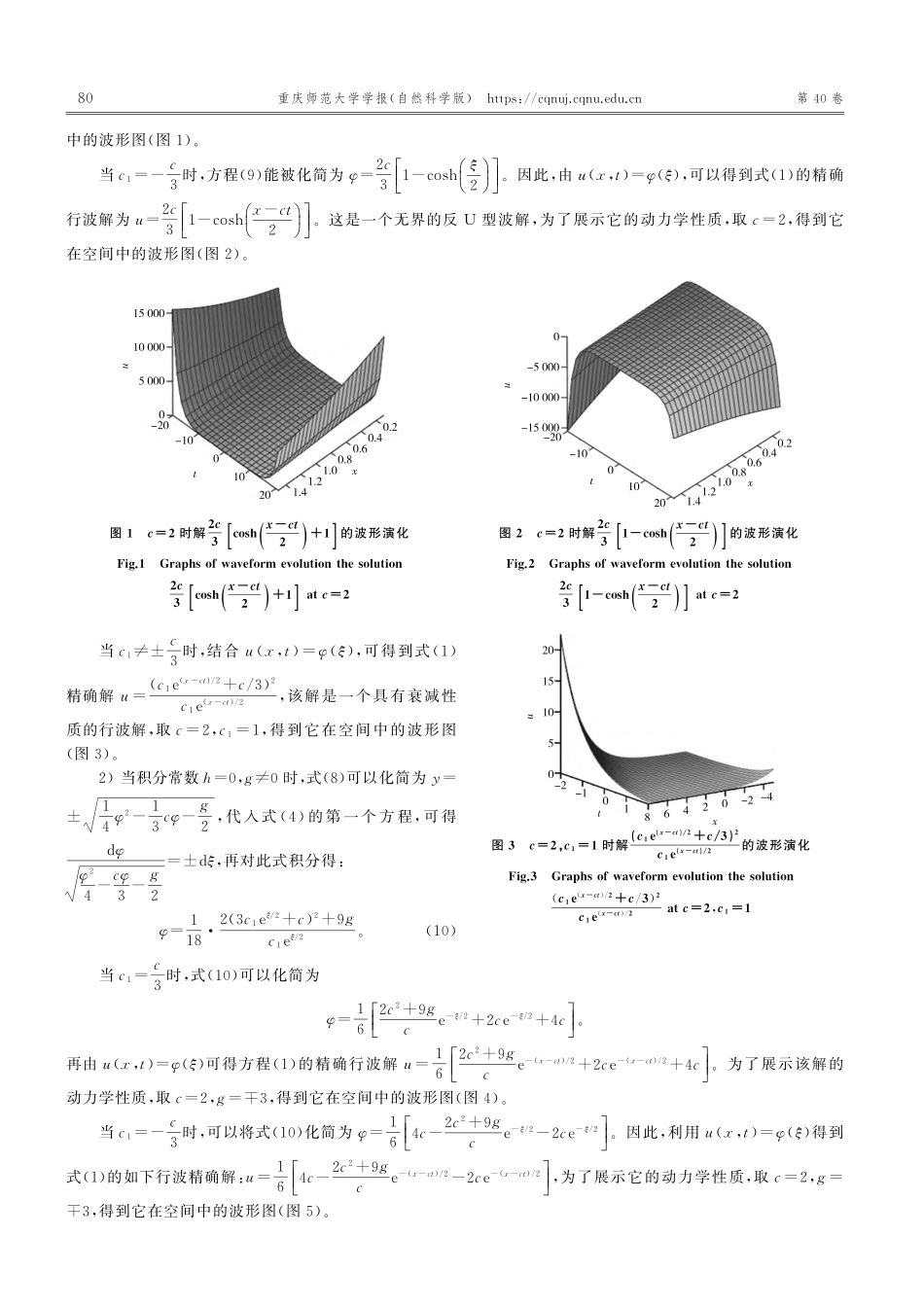
2023年5月重庆师范大学学报(自然科学版)May2023第40卷第3期JournalofChongqingNormalUniversity(NaturalScience)Vol.40No.3DOI:10.11721/cqnuj20230310非线性色散波K(2,2)方程的精确解及动力学性质*吴春(重庆师范大学数学科学学院,重庆401331)摘要:【目的】研究了非线性色散波K(2,2)方程的行波解问题。【方法】利用行波变换研究了非线性色散波K(2,2)方程的行波解问题。【结果】获得了非线性色散波K(2,2)方程的各种精确行波解,并讨论了这些解的动力学性质。通过图像模拟,直观地展示了部分精确解的动力学行为和动力学演化现象。【结论】研究发现部分解具有奇异性质,与现有文献中的结果相比,获得的精确解都是新结果,而且求解方法和技巧较之前文献中的要简便许多。关键词:非线性色散波K(2,2)方程;行波变换;精确解中图分类号:O175.29文献标志码:A文章编号:1672-6693(2023)03-0078-08对非线性波的研究起源于19世纪苏格兰工程师Russell对非线性波(即孤立波)的发现。随着社会的发展和科技的进步,科研人员对非线性波的研究逐渐深入,最终发现:波形在传播中是陡峭还是光滑,与所研究的问题中是否存在色散现象和非线性现象有着直接的联系。比如,Yan[1-2]研究了K(m,n,k)方程um-1ut+a(un)x+b(uk)xxx=0,(n,k≠1),获得了上述方程的紧波解、孤立波解以及周期波解。Yan[2]还通过作变换获得了以上方程的Jacobi椭圆函数解。特别地,当m=1,n=k=2时,以上K(m,n,k)方程就变成了K(2,2)方程。近些年来,田立新等人[3-5]采用动力系统面分支法研究了下列K(2,2)方程的各种行波解及动力学性质:ut+(u2)x-(u2)xxx=0,(1)其中负色散项表示收缩色散。这些解的形状有尖峰型孤立(尖峰波)、周期尖峰波、光滑波等。这些现象被看作非线性收缩色散与非线性对流之间相互作用而产生的结果。关于K(2,2)更多的研究结果,详见参考文献[6-8]及相关引用文献。著名的Camassa-Holm方程[9]ut-uxxt+3uux=2uxuxx+uuxxx(后简称CH方程)与本文研究的K(2,2)方程具有类似的结构,且与方程(1)含有相同的非线性项,只是非线性项的系数略有不同。早期的研究者们通过不同的方法获得了CH方程的大量精确解。例如,Camassa等人[10]通过动力系统面分支法获得了该方程的尖峰波(peakon)解;Liu等人[11]和Li等人[12]通过平面动力系统分支方法获得了该方程的周期尖峰波解;Li等人[13]进一步证明了周期尖峰波解的收敛性;Liu等人[14]用Jacobian椭圆函数法获得了该方程的尖峰波和孤立尖波解,并通过因式分解的方法获得了该方程具有参数形...