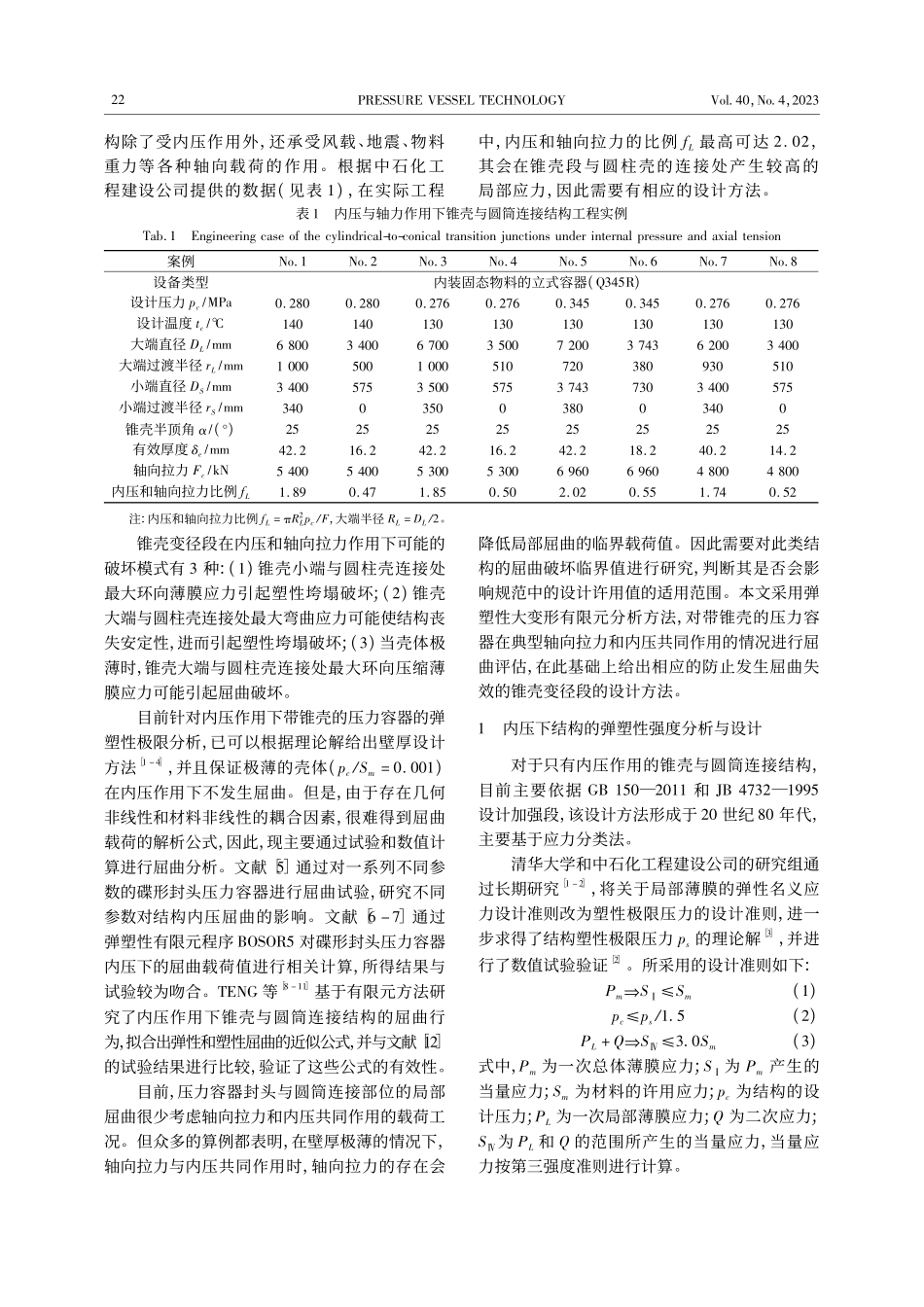
第40卷第4期压力容器2023年4月doi:■■■■■■■■■■■■■■■■■■■■10.3969/j.issn.1001-4837.2023.04.004设计计算内压与轴向拉力作用下锥壳与圆筒连接结构的屈曲分析刘佳锋,向志海,薛明德(清华大学工程力学系,北京100084)摘要:在我国压力容器标准GB150—2011《压力容器》和行业标准JB4732—1995《钢制压力容器———分析设计标准》(2005年确认)中,锥壳大端或小端与圆柱壳相连接结构的设计方法只考虑了塑性垮塌和丧失安定两种失效模式,并认为通常情况下结构不会发生屈曲。但是当结构的壁厚很薄,并且受到很大的轴向拉力时,有必要讨论是否会发生屈曲。为此,基于弹塑性大变形有限元法,分析了内压和轴向拉力按不同比例加载时,锥壳和圆筒连接结构的屈曲承载力,并以此提出了内压和轴向拉力组合作用下锥壳的屈曲判别式。计算结果表明,依据原有设计规范进行设计的锥壳结构有至少2.4倍的安全余量,所提出的屈曲判别式与数值试验结果吻合较好。关键词:压力容器;锥壳;分析设计准则;屈曲分析;多组载荷中图分类号:TH49;O344.3文献标志码:ABucklinganalysisofthecylindrical-to-conicaltransitionjunctionsunderinternalpressureandaxialtensionLIUJiafeng,XIANGZhihai,XUEMingde(DepartmentofEngineeringMechanics,TsinghuaUniversity,Beijing100084,China)Abstract:InthepressurevesselstandardsGB150—2011PressureVesselsandJB4732—1995SteelPressureVessels—DesignbyAnalysis(Confirmedin2005),onlyplasticcollapseandshakedownlimitareconsideredinthedesignofthecylindrical-to-conicaltransitionjunctions,and.Itisconsideredthatthestructurewillnotbuckleingeneralcase.However,itisnecessarytodiscusswhetherbucklingwilloccurornotwhenthewallofthestructureisextremelythinunderaverylargeaxialtension.Forthis,thebucklingcapacityofthecylindrical-to-conicaltransitionjunctionsunderinternalpressureandaxialtensionappliedindifferentproportionswasanalyzedbytheelastic-plasticlargedeformationfiniteelementmethod.Thecorrespondingbucklingcriterionfortheconicalshellwasproposedunderthecombinedactionofinternalpressureandaxialtension.Theresultsshowthatthecylindrical-to-conicaltransitionjunctionsdesignedaccordingtotheoriginaldesignspecificationhasasafetymarginofatleast2....