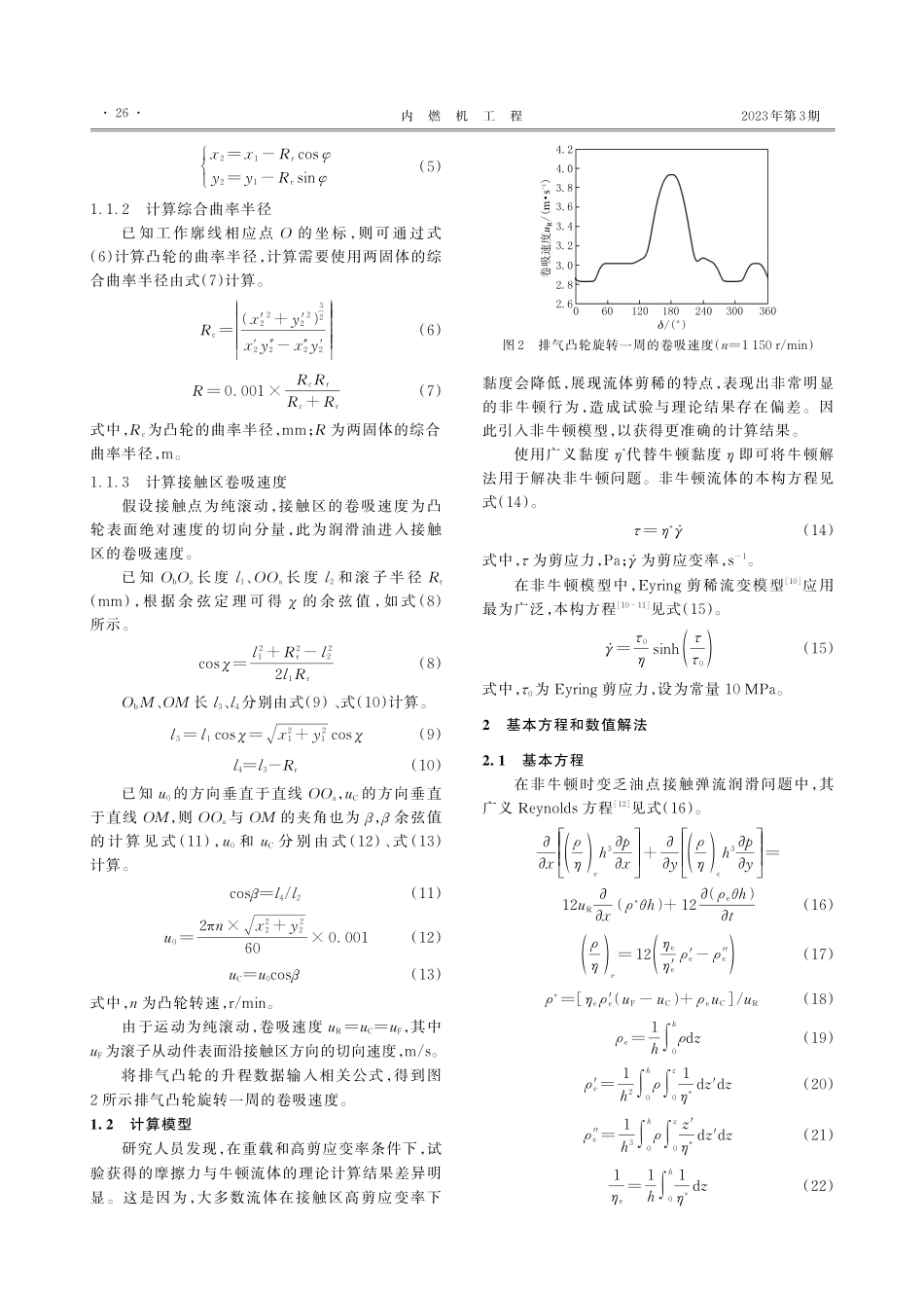
第44卷第3期2023年6月Vol.44No.3June2023内燃机工程ChineseInternalCombustionEngineEngineering内燃机凸轮–滚子接触副时变非牛顿润滑分析晁珅1,2,刘成1,2,朱桂香1,2,高园杰3,郭峰3,李书义3(1.内燃机可靠性国家重点实验室,潍坊261061;2.潍柴动力股份有限公司,潍坊261061;3.青岛理工大学机械与汽车工程学院,青岛266520)LubricationAnalysisforTransientNon-NewtonianoftheCam–RollerPairinAnInternalCombustionEngineCHAOShen1,2,LIUCheng1,2,ZHUGuixiang1,2,GAOYuanjie3,GUOFeng3,LIShuyi3(1.StateKeyLaboratoryofEngineReliability,Weifang261061,China;2.WeichaiPowerCo.,Ltd.,Weifang261061,China;3.SchoolofMechanicalandAutomotiveEngineering,QingdaoUniversityofTechnology,Qingdao266520,China)Abstract:Anon-Newtonianstarvedtransientlubricationmodelofthecam–rollerpairinaninternalcombustionenginewasestablished,andthefilmthicknessratiowasusedtoassessthelubricationbehaviorateachcamrotationangle.Thelubricationofthecontactpairinthecaseofrollerslippagewasstudied,andtheinfluenceofslide–rollratiosonthefilmthicknessratioswasanalyzed.Itwasfoundthatthelargertheslide–rollratios,themorethecamrotationangleswiththefilmthicknessratioslessthan1.5.Thentheinfluenceofoilsupplyonthefilmthicknessratioswasdiscussed,andthecriticaloillayerthicknessatwhichthefilmthicknessratiosdecreasedsignificantlywasgiven.Finally,thechangesofthelubricatingviscositiesattheactualworkingtemperatureswereconsideredtoexploretheinfluenceofvariousviscositiesonthelubricatingstates.Itwasfoundthatwhentheviscositywas0.01Pa·s,thelubricationstateofsomeanglesenteredboundarylubrication.Incertainworkingconditionsthefrictioncoefficientsdecreasedgraduallywiththedecreaseoflubricatingviscosities.摘要:建立了内燃机凸轮–滚子副非牛顿时变乏油润滑模型,用膜厚比讨论每个凸轮旋转角度的润滑状态。首先,研究滚子打滑情况下接触副的润滑问题,分析了不同滑滚比对膜厚比的影响,发现滑滚比越大,膜厚比小于1.5的凸轮旋转角度越多。讨论了供油膜厚对膜厚比的影响,获得了膜厚比大幅下降的临界供油膜厚。最后,考虑实际工作温度下润滑油黏度的变化,探究了不同黏...