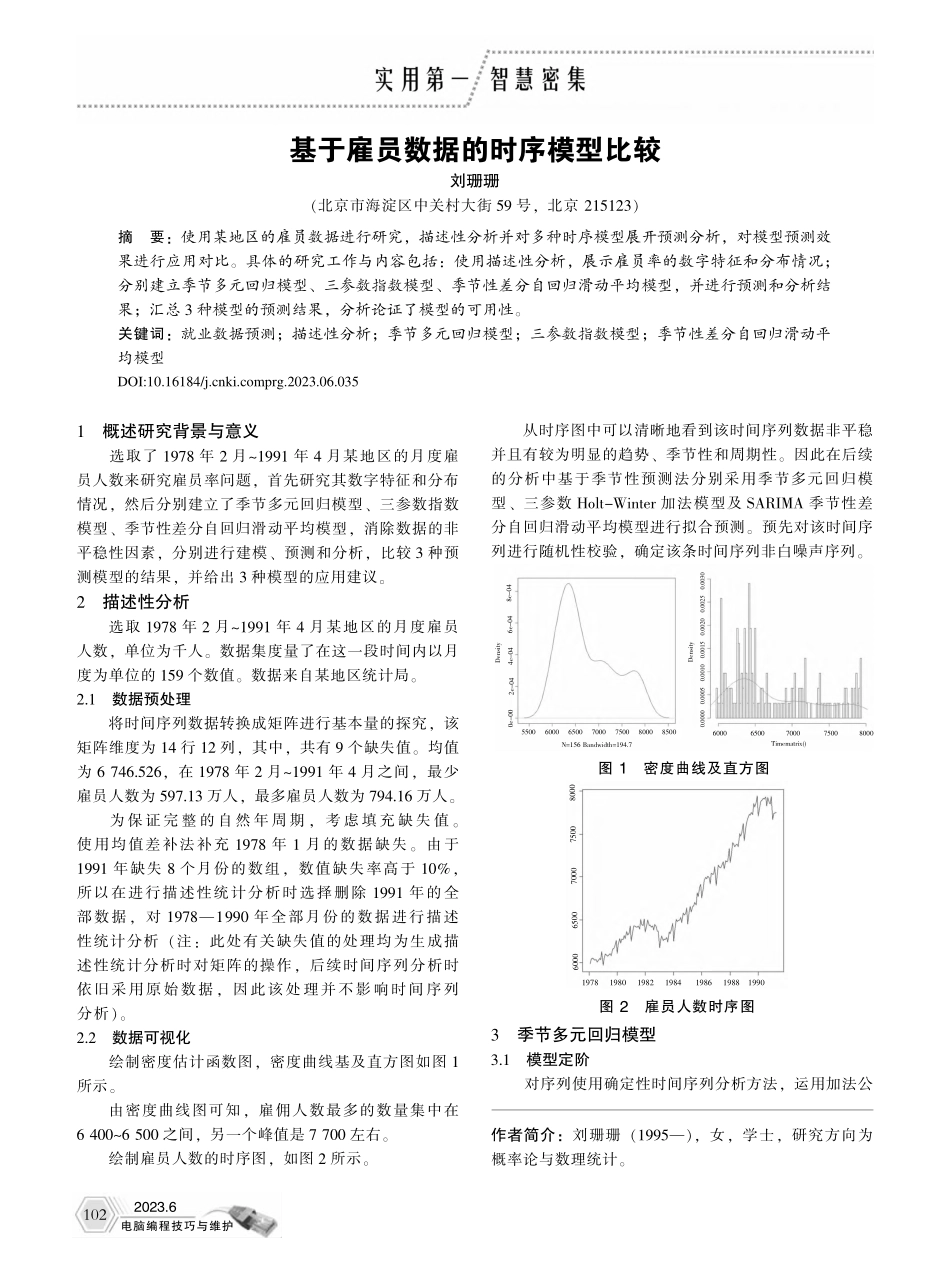
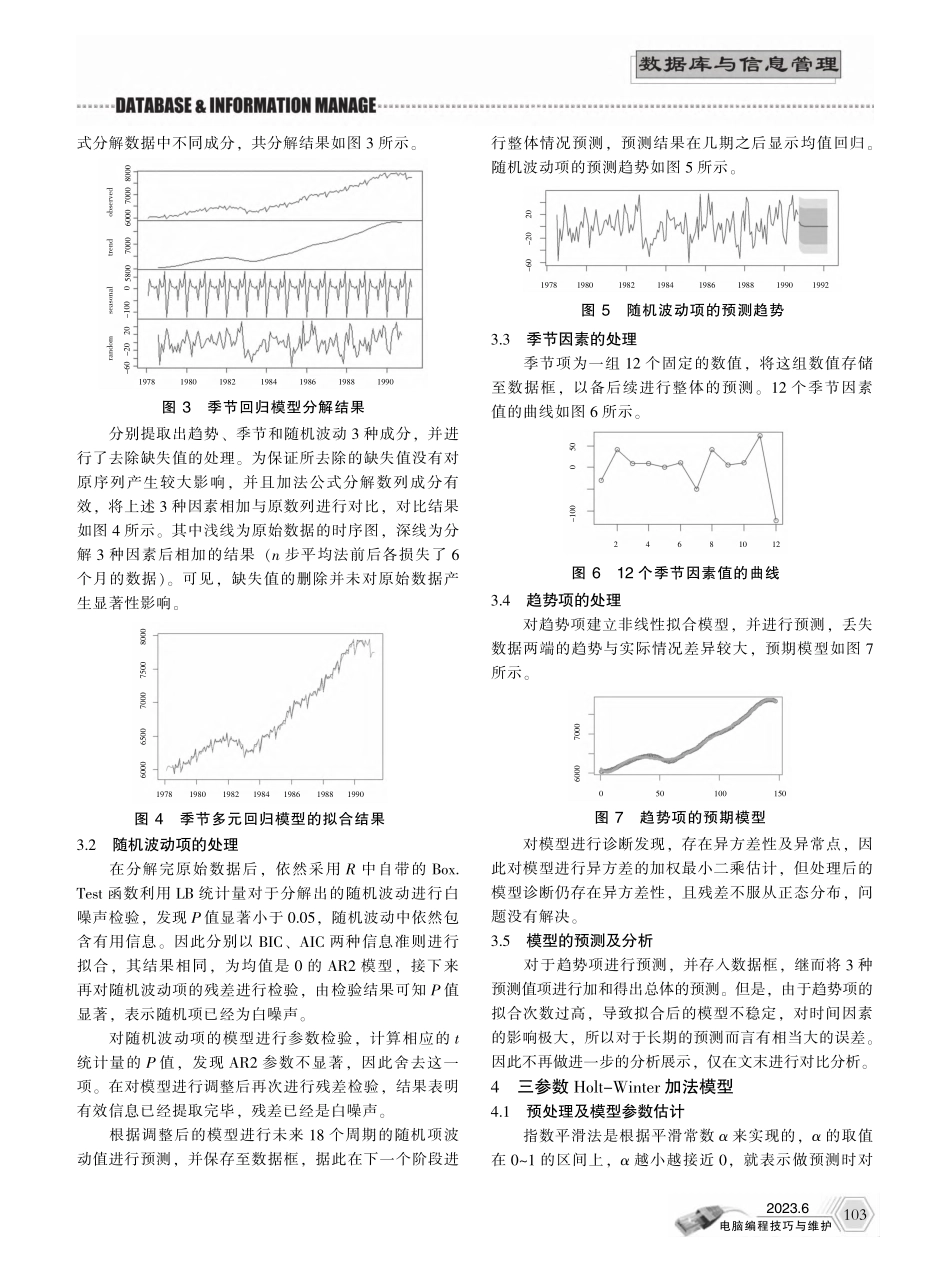
2023.6电脑编程技巧与维护图1密度曲线及直方图1概述研究背景与意义选取了1978年2月~1991年4月某地区的月度雇员人数来研究雇员率问题,首先研究其数字特征和分布情况,然后分别建立了季节多元回归模型、三参数指数模型、季节性差分自回归滑动平均模型,消除数据的非平稳性因素,分别进行建模、预测和分析,比较3种预测模型的结果,并给出3种模型的应用建议。2描述性分析选取1978年2月~1991年4月某地区的月度雇员人数,单位为千人。数据集度量了在这一段时间内以月度为单位的159个数值。数据来自某地区统计局。2.1数据预处理将时间序列数据转换成矩阵进行基本量的探究,该矩阵维度为14行12列,其中,共有9个缺失值。均值为6746.526,在1978年2月~1991年4月之间,最少雇员人数为597.13万人,最多雇员人数为794.16万人。为保证完整的自然年周期,考虑填充缺失值。使用均值差补法补充1978年1月的数据缺失。由于1991年缺失8个月份的数组,数值缺失率高于10%,所以在进行描述性统计分析时选择删除1991年的全部数据,对1978—1990年全部月份的数据进行描述性统计分析(注:此处有关缺失值的处理均为生成描述性统计分析时对矩阵的操作,后续时间序列分析时依旧采用原始数据,因此该处理并不影响时间序列分析)。2.2数据可视化绘制密度估计函数图,密度曲线基及直方图如图1所示。由密度曲线图可知,雇佣人数最多的数量集中在6400~6500之间,另一个峰值是7700左右。绘制雇员人数的时序图,如图2所示。从时序图中可以清晰地看到该时间序列数据非平稳并且有较为明显的趋势、季节性和周期性。因此在后续的分析中基于季节性预测法分别采用季节多元回归模型、三参数Holt-Winter加法模型及SARIMA季节性差分自回归滑动平均模型进行拟合预测。预先对该时间序列进行随机性校验,确定该条时间序列非白噪声序列。3季节多元回归模型3.1模型定阶对序列使用确定性时间序列分析方法,运用加法公作者简介:刘珊珊(1995—),女,学士,研究方向为概率论与数理统计。基于雇员数据的时序模型比较刘珊珊(北京市海淀区中关村大街59号,北京215123)摘要:使用某地区的雇员数据进行研究,描述性分析并对多种时序模型展开预测分析,对模型预测效果进行应用对比。具体的研究工作与内容包括:使用描述性分析,展示雇员率的数字特征和分布情况;分别建立季节多元回归模型、三参数指数模型、季节性差分自回归滑动平均模型,并进行预测和分析结果;汇总3种模型的预测结果,分析论证了模...