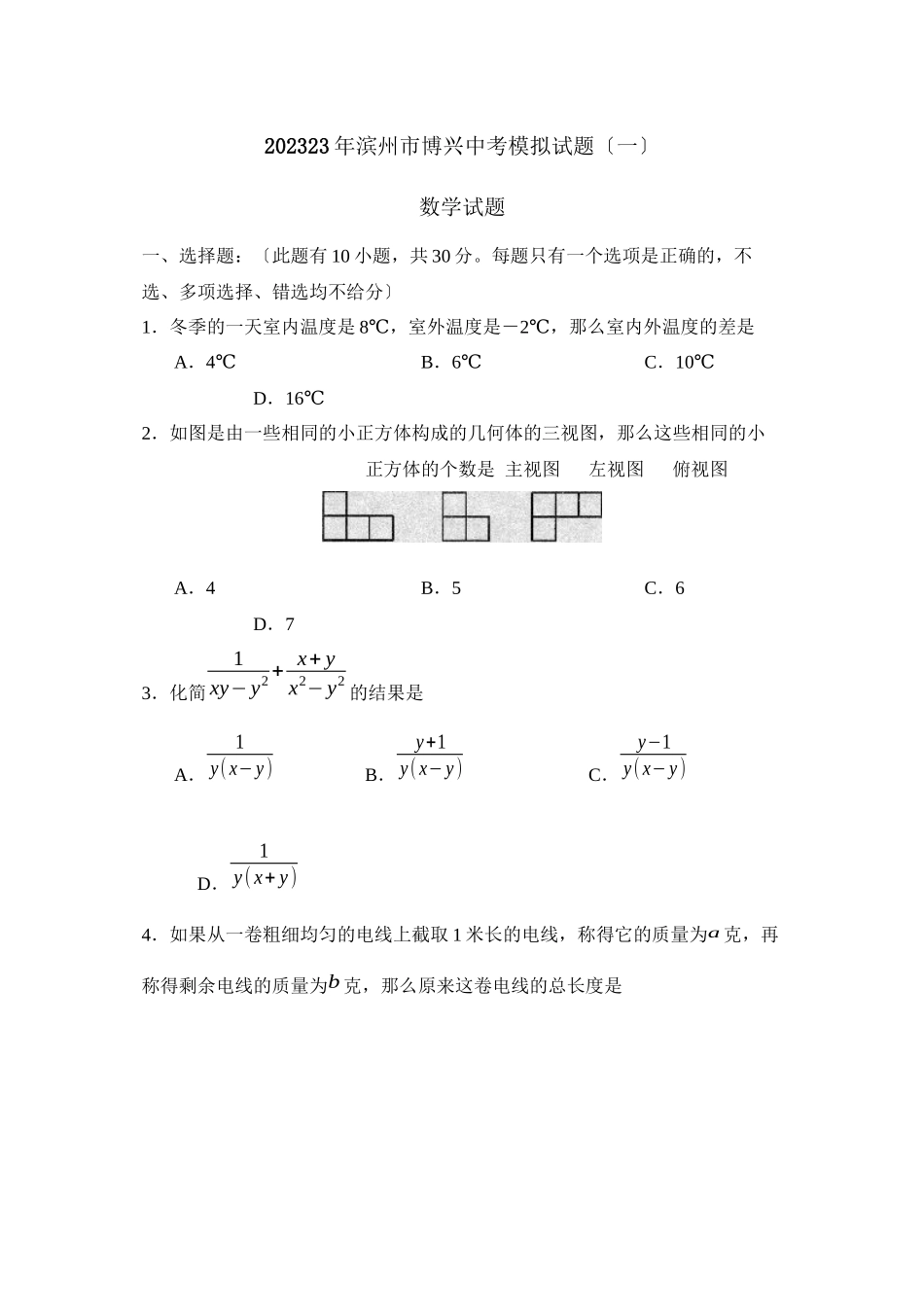
202323年滨州市博兴中考模拟试题〔一〕数学试题一、选择题:〔此题有10小题,共30分。每题只有一个选项是正确的,不选、多项选择、错选均不给分〕1.冬季的一天室内温度是8℃,室外温度是-2℃,那么室内外温度的差是A.4℃B.6℃C.10℃D.16℃2.如图是由一些相同的小正方体构成的几何体的三视图,那么这些相同的小正方体的个数是主视图左视图俯视图A.4B.5C.6D.73.化简1xy−y2+x+yx2−y2的结果是A.1y(x−y)B.y+1y(x−y)C.y−1y(x−y)D.1y(x+y)4.如果从一卷粗细均匀的电线上截取1米长的电线,称得它的质量为a克,再称得剩余电线的质量为b克,那么原来这卷电线的总长度是A.b+1a米B.(ba+1)米C.(a+ba+1)米D.(ab+1)米5.如图,⊙O是ABC的外接圆,连接OA、OC,⊙O的半径R=2,sinB=34,那么AC的长为A.3B.√7C.32D.346.小颖的家与学校的距离为s0千米,她从家到学校先以匀速v1跑步前进,后以匀速v2〔v2“〞、=“〞、<〞〕。13.杏花村现有188部,比2023年底的3倍还多17部,那么该村2023年底有部。14.假设矩形的面积为6,那么矩形的长y关于宽x〔x>0〕的函数关系式为。15.小明的身高是1.7m,他的影长是2m,同一时刻学校旗杆的影长是10m,那么旗杆的高是____m。16.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,那么DN+MN的最小值为。17.在解分式方程x2−2x+xx2−2=2时,假设设了x2−2x=y,那么原分式方程可化为。1...