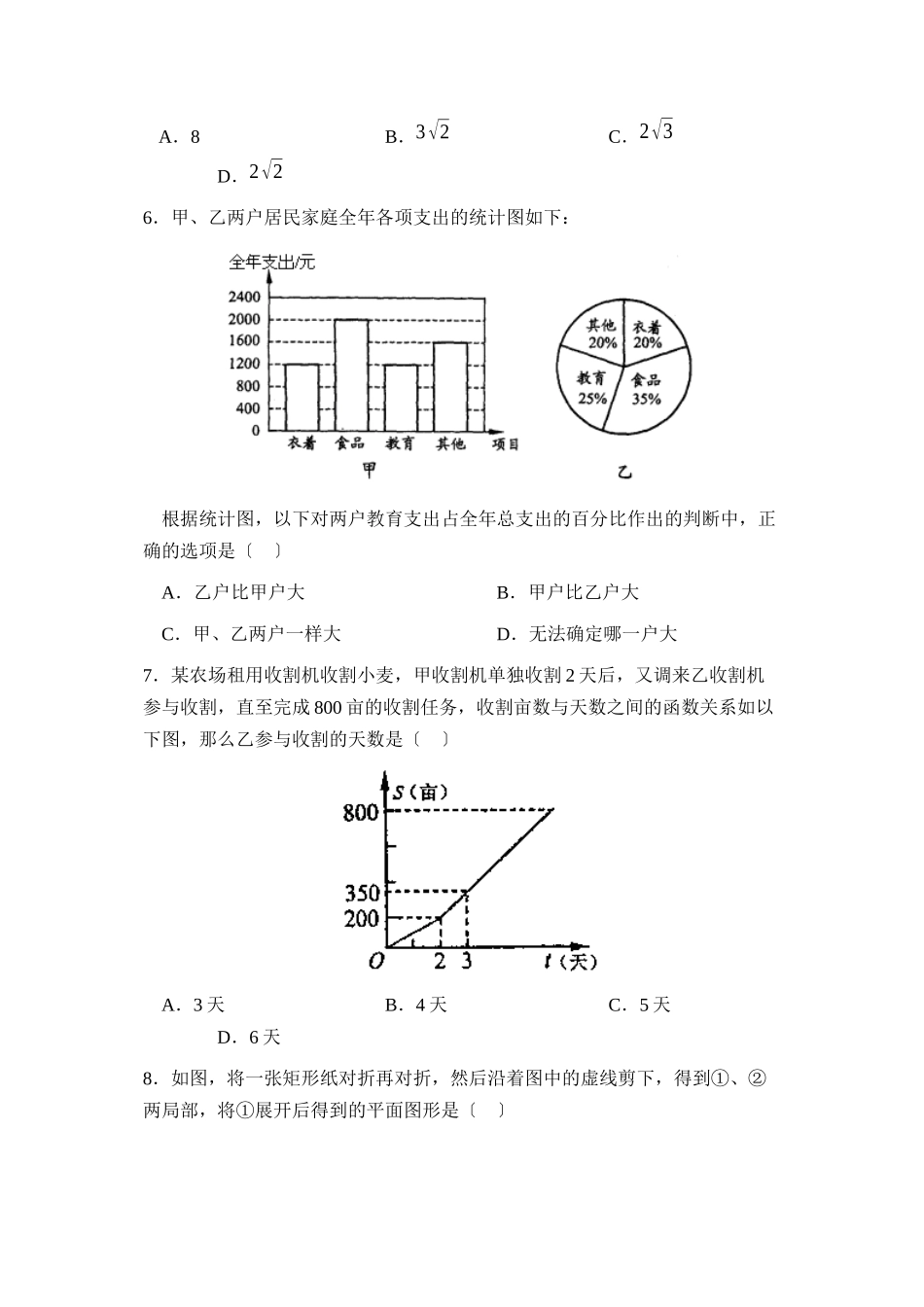
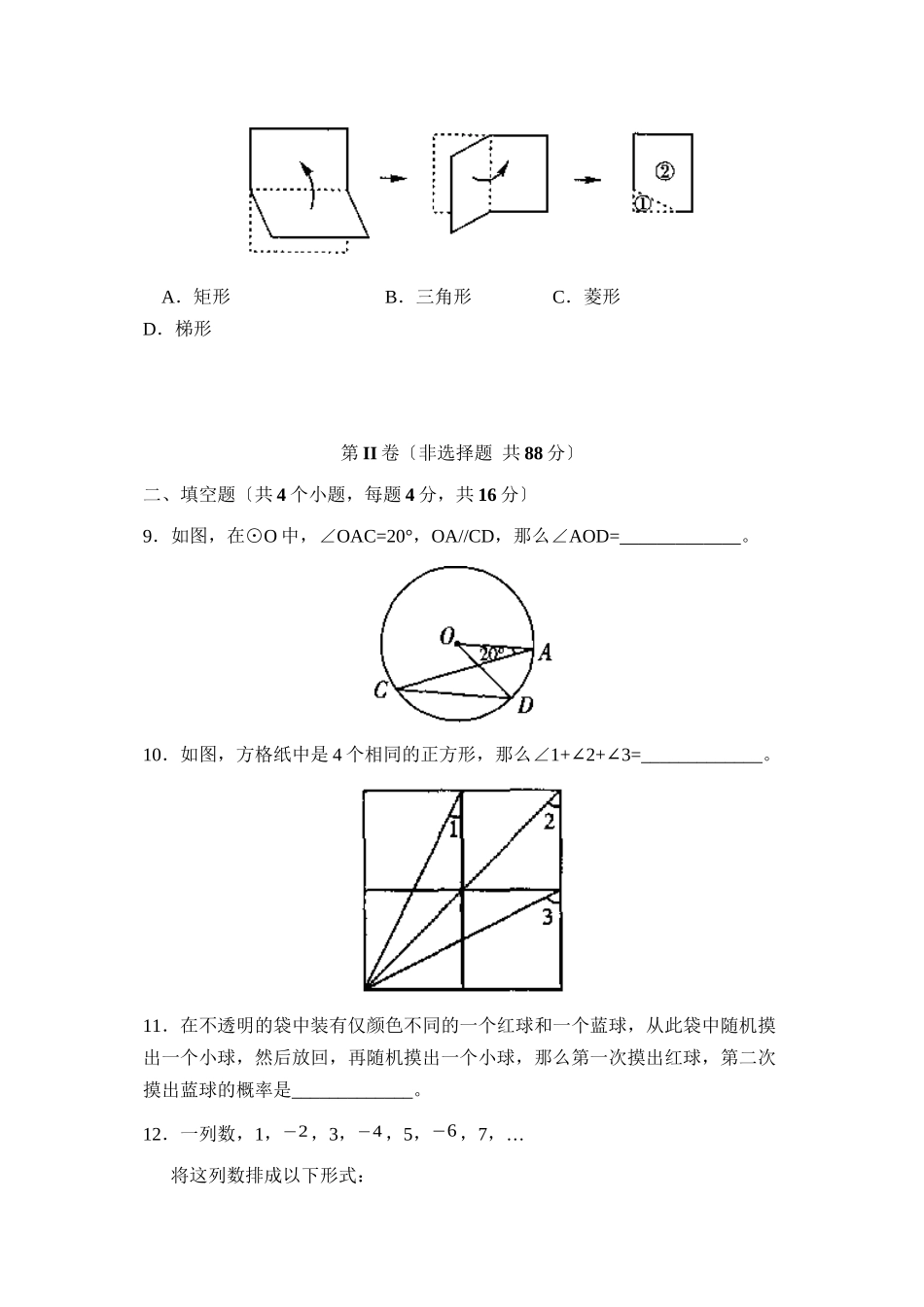
202323年北京市宣武区初三下学期第一次质量检测数学试卷2023.5第I卷〔选择题共32分〕一、选择题〔共8个小题,每题4分,共32分〕以下各题均有四个选项,其中只有一个是符合题目要求的。1.−4的绝对值是〔〕A.4B.−4C.2D.±42.△ABCDEF∽△,AB:DE=1:2,那么△ABC△DEF的周长比等于〔〕A.2:1B.4:1C.1:2D.1:43.如果要用正三角形和正方形两种图形镶嵌平面,那么至少需要〔〕A.三个正三角形,三个正方形B.两个正三角形,三个正方形C.两个正三角形,两个正方形D.三个正三角形,两个正方形4.如以下图几何体的左视图是〔〕5.有一个数值转换器,原理如下:当输入的x为64时,输出的y是〔〕A.8B.3√2C.2√3D.2√26.甲、乙两户居民家庭全年各项支出的统计图如下:根据统计图,以下对两户教育支出占全年总支出的百分比作出的判断中,正确的选项是〔〕A.乙户比甲户大B.甲户比乙户大C.甲、乙两户一样大D.无法确定哪一户大7.某农场租用收割机收割小麦,甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务,收割亩数与天数之间的函数关系如以下图,那么乙参与收割的天数是〔〕A.3天B.4天C.5天D.6天8.如图,将一张矩形纸对折再对折,然后沿着图中的虚线剪下,得到①、②两局部,将①展开后得到的平面图形是〔〕A.矩形B.三角形C.菱形D.梯形第II卷〔非选择题共88分〕二、填空题〔共4个小题,每题4分,共16分〕9.如图,在⊙O中,∠OAC=20°,OA//CD,那么∠AOD=_____________。10.如图,方格纸中是4个相同的正方形,那么∠1+2+3=_____________∠∠。11.在不透明的袋中装有仅颜色不同的一个红球和一个蓝球,从此袋中随机摸出一个小球,然后放回,再随机摸出一个小球,那么第一次摸出红球,第二次摸出蓝球的概率是_____________。12.一列数,1,−2,3,−4,5,−6,7…,将这列数排成以下形式:中间用虚线围的一列数,从上至下依次为1、5、13、25……、,按照上述规律排下去,那么虚线框中的第7个数是_____________。三、解答题:〔共5个小题,每题4分,共20分〕13.计算:(√2−1)0×(12)−1+√2×sin45°。14.解方程:3x−1=5x+1。15.解不等式组:{6(x−2)≥x+3①¿¿¿¿16.如图,AC交BD于点O,请你从下面三项中选出两个作为条件,另一个为结论,写出一个真命题,并加以证明。〔1〕OA=OC〔2〕OB=OD〔3〕AB//DC17.某地某时刻太阳光线与水平线的夹角为31°,此时在该地测得一幢楼房在水平地面...