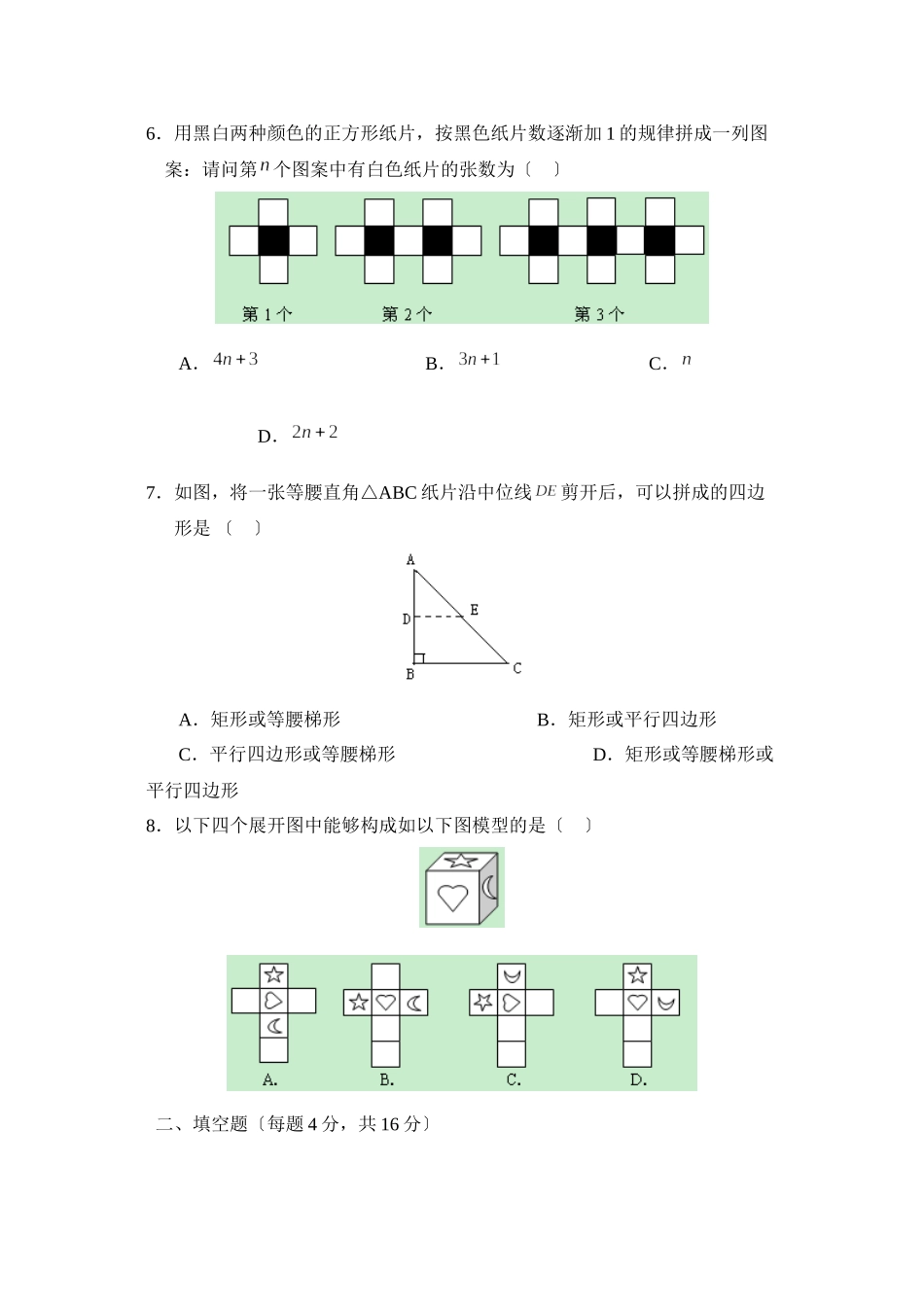
2023年北京市丰台区初三年级二模试卷数学一、选择题〔每题4分,共32分〕1.以下计算正确的选项是〔〕A.B.C.D.2.北京市申办2023年奥运会,得到了全国人民的热情支持.据统计,某日北京申奥网站的访问人次为,用四舍五入法取近似值保存两个有效数字,得〔〕A.B.C.D.3.某校为了了解240名初三学生的体重情况,从中抽取50名学生进行测量,以下说法正确的选项是〔〕A.总体是240B.样本容量是50C.样本是50名D.个体是每个学生4.假设分式3x2−6xx−2的值为0,那么x的值为〔〕A.0B.2C.-2D.0或25.的图象如以下图,那么的图象一定过〔〕A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限6.用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一列图案:请问第个图案中有白色纸片的张数为〔〕A.B.C.D.7.如图,将一张等腰直角△ABC纸片沿中位线剪开后,可以拼成的四边形是〔〕A.矩形或等腰梯形B.矩形或平行四边形C.平行四边形或等腰梯形D.矩形或等腰梯形或平行四边形8.以下四个展开图中能够构成如以下图模型的是〔〕二、填空题〔每题4分,共16分〕9.b、m是实数,|m−2b|+√b−1=0,那么m−b的值为.10.如图,AB∥CD,∠C=35°,BC平分∠ABE,那么∠ABE为度.11.假定鸟卵孵化后,雏鸟为雌鸟与为雄鸟的概率相同。如果三枚卵全部成功孵化,那么三只雏鸟中恰有两只雄鸟的概率为.12.在数学中,为了简便计算记1!=1,2!=2×1,3!=3×2×1……,,n!=.那么.三、解答题〔共5个小题,共24分〕13.〔4分〕计算:√12−(12)−1−tan60°+3√−8.14.〔4分〕△在平面直角坐标系中的位置如以下图,现将△ABC经过两次变换:第一次是作出△ABC关于y轴对称的△A1B1C1;再将△A1B1C1向下平移4个单位长度,得到△A2B2C2.请你在下面的网格中画出平移后的△A2B2C2.〔不写作法,保存作图痕迹,指明结果〕15.〔5分〕先化简再求值:a−1a+2⋅a2−4a2−2a+1÷1a2−1其中满足.16.〔5“分〕为响应承办绿色奥运〞的号召,某班组织局部同学义务植树棵,由于同学们的积极参与,实际参加的人数比原方案增加了,结果每人比原方案少栽了棵,问实际有多少人参加了这次植树活动?17.〔6分〕一次函数的图象与反比例函数的图象相交,其中一个交点的纵坐标为-4.〔1〕求两个函数的解析式;〔2〕结合图象求出当时,的取值范围.18.(本小题总分值5分):关于的一元二次方程.求证:不管取何值时,方程总有两个不...