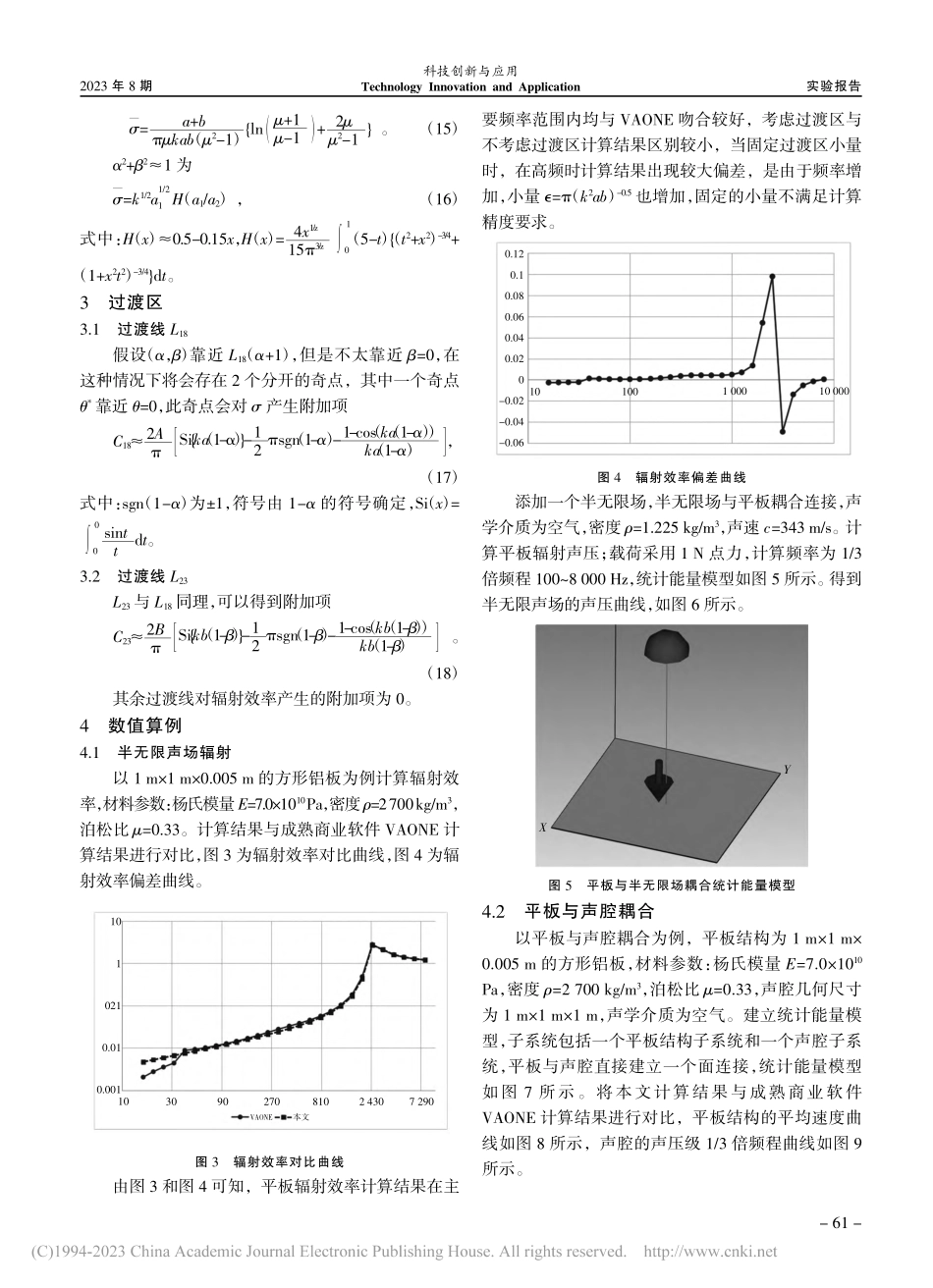
实验报告科技创新与应用TechnologyInnovationandApplication2023年8期矩形平板的声辐射效率计算钟策,陈赫(上海索辰信息科技股份有限公司,上海201204)振动结构的声辐射效率是其声辐射性能的一个重要表征参量,反映了振动结构向周围介质中辐射声能量的能力,是工程技术人员在进行声学结构设计时需要考虑的重要参数。其中平板的辐射效率计算是统计能量分析方法的基础问题,可用于平板与声腔耦合结构的声振问题求解。Xie等[1]使用瑞利积分求得球坐标系下远场任意一点的声强,再将声强对球面进行积分,得到了矩形简支板各阶模态辐射效率的解析表达式。梁健等[2]推导了带刚性障板的平板各阶弯曲振动模态的声辐射效率幂级数表达式,计算了不同边界条件下平板的声辐射效率。任惠娟等[3]通过声强对辐射面积分,得到了四边简支矩形板的模态辐射声功率的精确解析表达式,并采用了十节点的高斯-勒让得求积法进行数值计算,计算精度较高。张凯等[4]基于Mindlin厚板理论建立了四边简支矩形平板的振动声辐射数学计算模型,通过Rayleigh积分法得到模态声辐射系数,并得到结论:由于Mindlin厚板模型考虑了板的横向剪切变形和转动惯量,其动力学计算结果比经典薄板理论更精确,但由于声辐射仅与平板的横向振动相关,因此2种模型计算出来的平均辐射效率没有明显区别。1辐射效率积分假设一个面积为S(0
0的半无限大空间。基于Rayleigh积分,板对空间的时域平均辐射功率为式中:k=ω/c为声场波数,r2=x-x()′2+y-y()′2。对于相同面积和均方速度的刚性板,任一模态的辐射功率Prad的定义为P=ρ0cab,其中为板对于时间和空间的均方速度。对于简支板,板的模态振型可表示为f(x,y)=constant×sin(kxx)×sin(kyy),(2)式中:kx=mπ/a,ky=nπ/b分别表示x和y2个方向的波数分量。对波数进行无量纲化α=kxk=mπka,β=kyk=nπkb。(3)板的辐射效率σ可表示为第一作者简介:钟策(1991-),男,博士,研发部副总监。研究方向为流体,流固耦合,声学。摘要:平板的辐射效率计算是统计能量分析方法的基础问题。该文基于Rayleigh积分推导四边简支平板结构的声辐射效率积分表达式,并对奇异点处进行近似处理。最后通过数值算例计算,并与成熟商业软件VAONE进行对比,较高频率下...