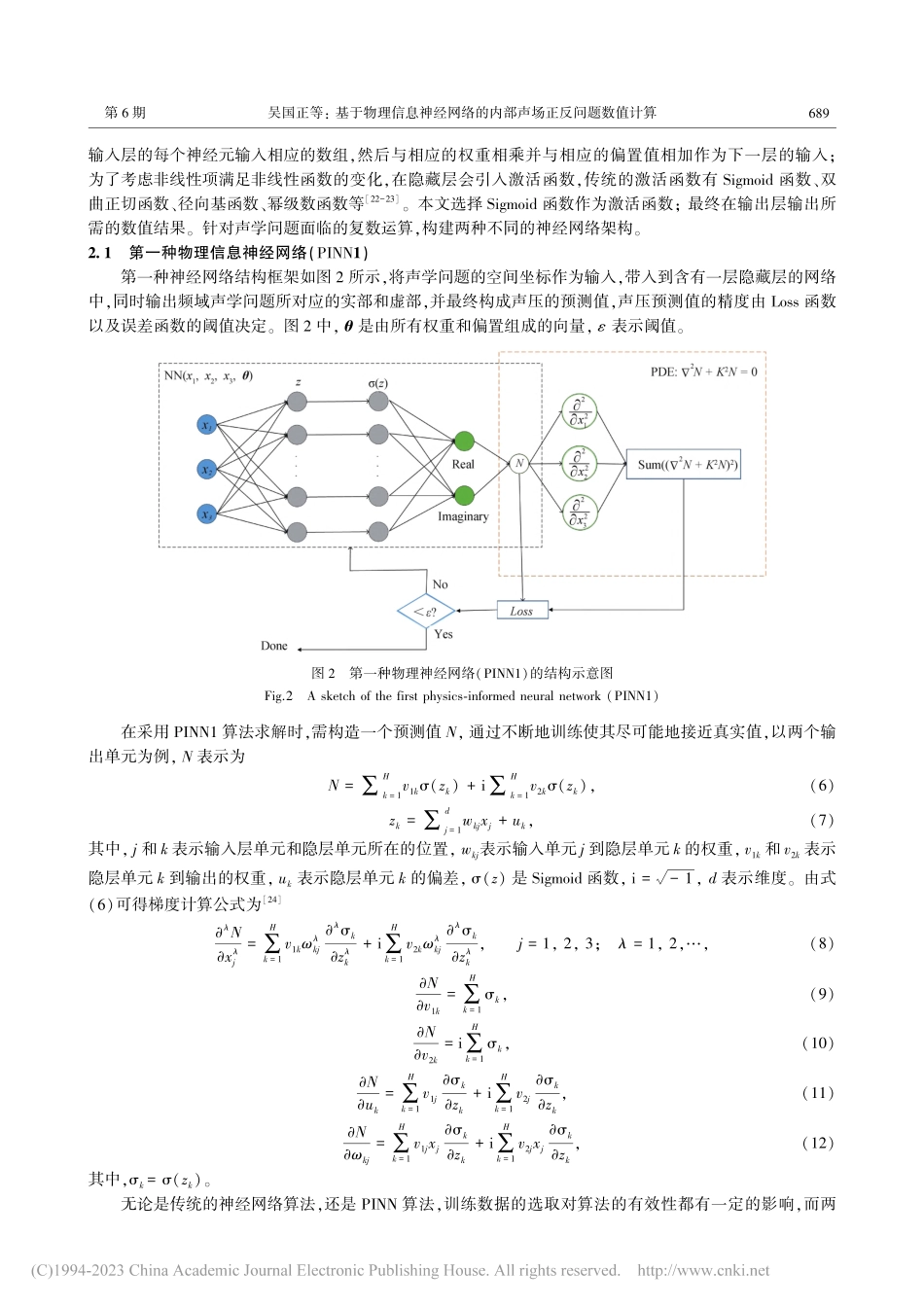
第39卷第6期2022年11月计算物理CHINESEJOURNALOFCOMPUTATIONALPHYSICSVol.39,No.6Nov.,2022文章编号:1001⁃246X(2022)06⁃0687⁃12收稿日期:2022-02-25;修回日期:2022-06-09基金项目:国家自然科学基金(11802151)、山东省自然科学基金(ZR2019BA008)资助项目第一作者:吴国正,男,硕士生,研究方向为计算物理,E⁃mail:wgz980518@163.com∗通信作者:王发杰,男,博士,副教授,主要从事物理力学建模及仿真研究,E⁃mail:wfj1218@126.com基于物理信息神经网络的内部声场正反问题数值计算吴国正1,王发杰1,2,∗,程隋福1,张成鑫1(1.青岛大学机电工程学院,山东青岛266071;2.青岛大学多功能材料与结构力学研究院,山东青岛266071)摘要:针对频域内部声场正反问题的数值模拟,建立基于物理信息的神经网络架构。与基于数据驱动的神经网络不同,将声学问题的Helmholtz方程及其对应的边界条件引入神经网络,所建立的神经网络算法不仅能够反映训练数据样本的分布规律,而且也遵循由偏微分方程描述的物理定律。考虑到频域声学问题中含有复数部分,建立两种网络架构,并进行验证和比较分析。该方法无需网格划分和数值积分等繁琐的数值计算过程,可自由地处理不规则区域和非均匀分布情形。数值实验考察二维和三维复杂几何结构的声学正问题及反问题,结果表明所建立的物理信息神经网络算法具有较高的精确度、收敛性和鲁棒性。关键词:物理信息神经网络;声学问题;Helmholtz方程;正问题;反问题中图分类号:O369;O422;O242文献标识码:ADOI:10.19596/j.cnki.1001⁃246x.85200引言在很多工程领域中,都会伴随着声学问题的分析,由于测量技术的限制,部分边界条件或参数可能会出现无法获取的情况,因此声学问题又可被分为声学正问题和声学反问题。例如,已知物体的所有边界条件以及介质参数,求解其内部各点的声压值、声压级等,这类问题称之为声学正问题;当边界条件不能被完全获取时,或介质参数未知时,通过已知的数据反演出介质参数、未知边界数据等,这类问题称之为声学反问题。正问题是一种适定性问题,存在唯一的解,应用在很多领域,求解的方法相对成熟,主要是...