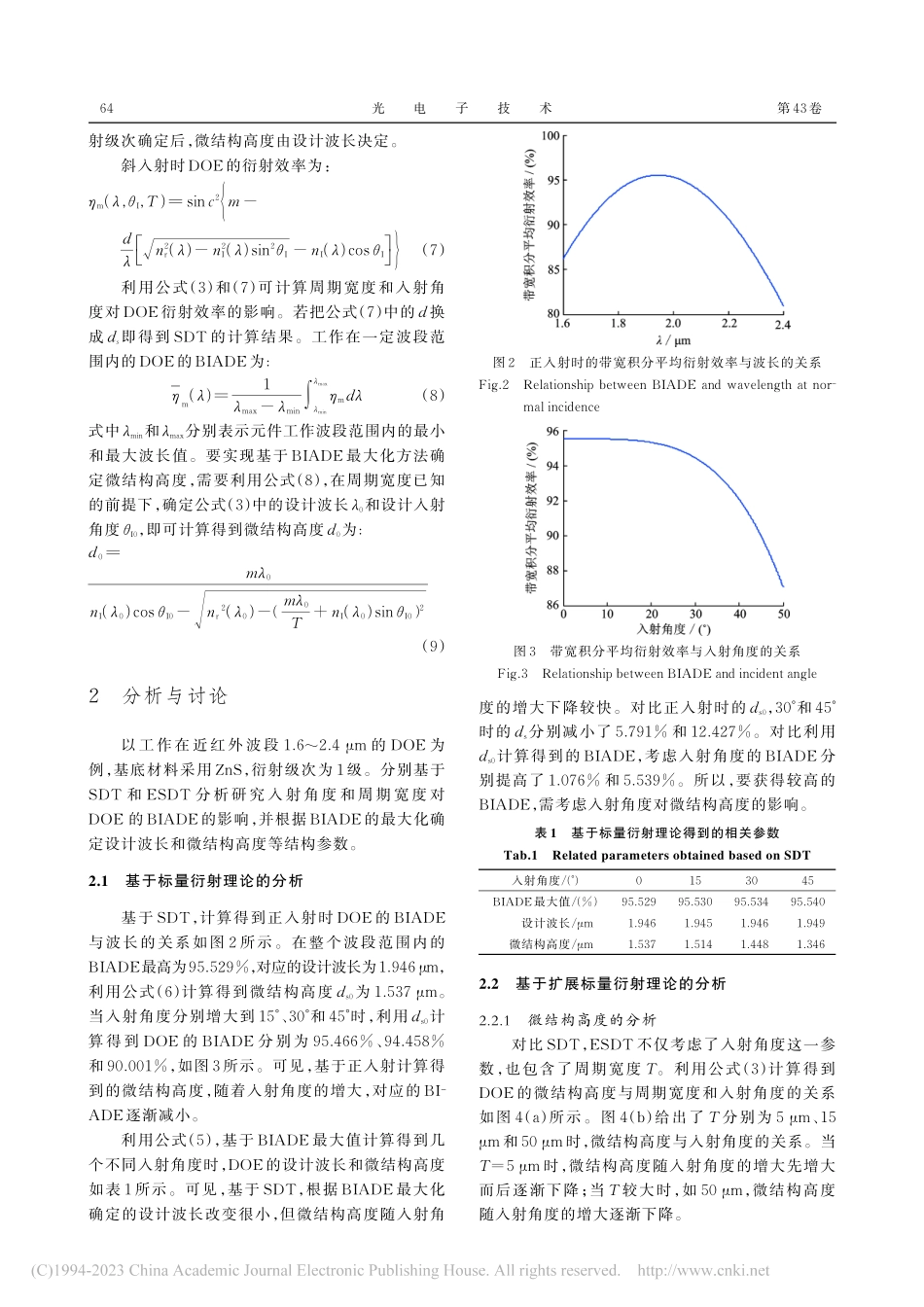
第43卷第1期2023年3月光电子技术OPTOELECTRONICTECHNOLOGYVol.43No.1Mar.2023基于扩展标量衍射理论的衍射光学元件设计∗杨亮亮∗∗,沈法华,赵琪,刘建利,赵勇兵(盐城师范学院物理与电子工程学院,江苏省智能光电器件与测控工程研究中心,盐城江苏224007)摘要:基于扩展标量衍射理论,建立了衍射光学元件的微结构高度与周期宽度和入射角度的理论关系模型,提出了不同入射角度时,利用带宽积分平均衍射效率最大化实现设计波长和微结构高度等结构参数的优化设计方法。以工作在近红外波段的衍射光学元件为例进行分析。结果表明:周期宽度一定时,入射角度的改变会引起基于带宽积分平均衍射效率最大化所确定的结构参数发生变化。该设计方法和结论可以用于指导衍射光学元件的设计。关键词:衍射光学;入射角度;衍射效率;微结构高度中图分类号:TN29;O436文献标志码:A文章编号:1005⁃488X(2023)01⁃0062⁃05DesignofDiffractiveOpticalElementBasedonExtendedScalarDiffractionTheoryYANGLiangliang,SHENFahua,ZHAOQi,LIUJianli,ZHAOYongbing(JiangsuProvinceIntelligentOptoelectronicDevicesandMeasurementControlEngineeringResearchCenter,SchoolofPhysicsandElectronicsEngineering,YanchengTeachersUniversity,YanchengJiangsu224007,CHN)Abstract:Basedontheextendedscalardiffractiontheory(ESDT),thetheoreticalmodeloftherelationshipbetweenthemicrostructureheight,theperiodwidthandtheincidenceangleofdiffractiveopticalelement(DOE)wasestablished.Theoptimaldesignmethodofthestructureparameters,suchasdesignwavelengthandmicrostructureheight,wasproposedbasedonthemaximizationoftheband⁃widthintegralaveragediffractionefficiency(BIADE)atdifferentincidentangles.ADOEworkingwithinthenearinfraredwavebandwastakenasanexample.Resultsindicatedthatwhentheperiodwidthwasdetermined,thechangeofincidentanglecouldcausethechangeofstructureparametersob⁃tainedbasedonthemaximizationofBIADE.ThedesignedmethodandconclusionscouldbeusedtoguidethedesignofDOE.Keywords:diffractiveoptics;incidentangle;diffractionefficiency;microstructureheightDOI:10.19453/j.cnki.1005⁃488x.2023.01.010收稿日期:2022-09-16∗基金项目:国家自然科学基金(61904158);江苏省智能光电器件与测控工程研...