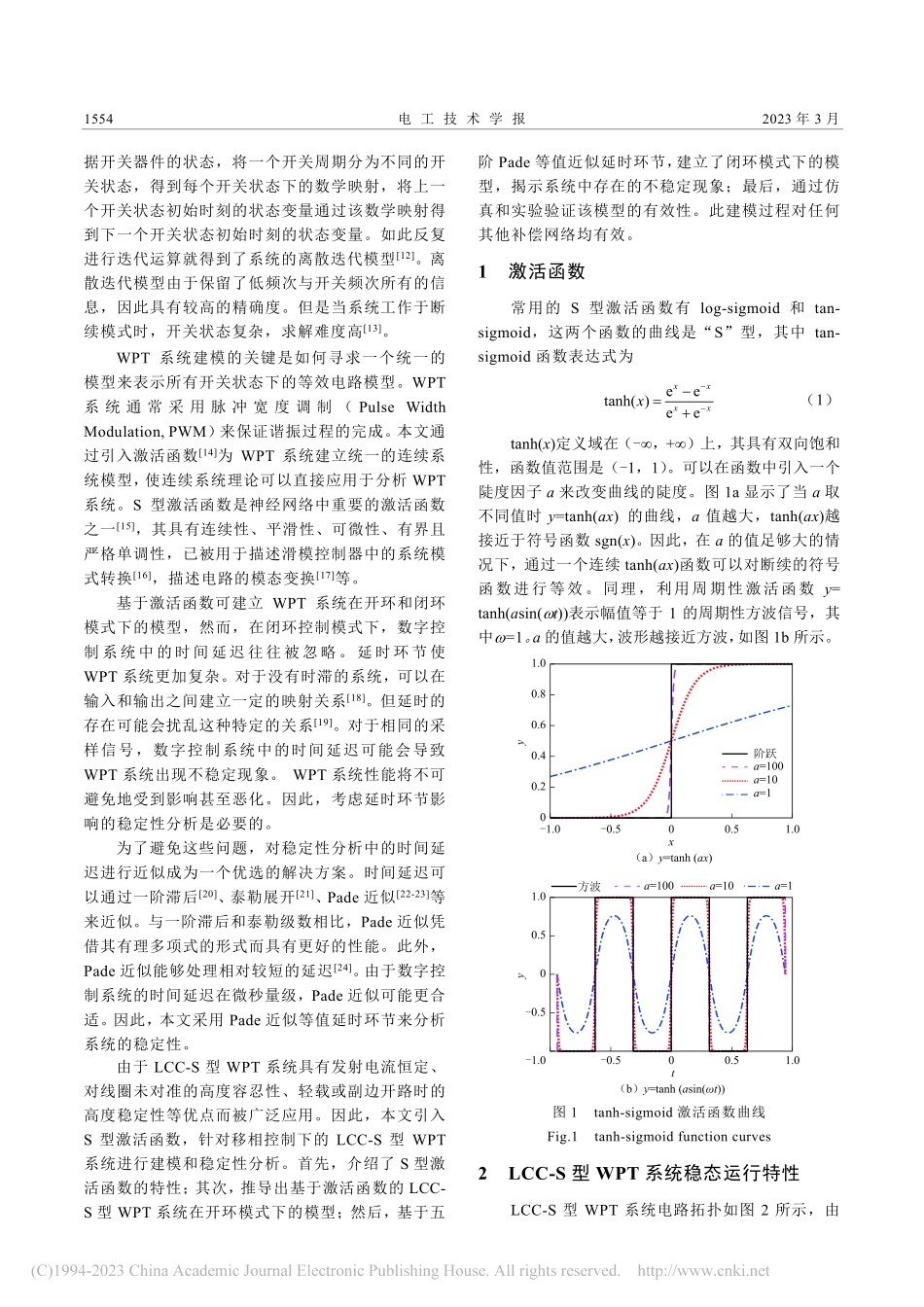
2023年3月电工技术学报Vol.38No.6第38卷第6期TRANSACTIONSOFCHINAELECTROTECHNICALSOCIETYMar.2023DOI:10.19595/j.cnki.1000-6753.tces.211722基于激活函数的LCC-S型无线电能传输系统建模和稳定性分析胡秀芳王跃吕双庆赵德林马天录(电力设备电气绝缘国家重点实验室(西安交通大学)西安710049)摘要基于电力电子器件的无线电能传输(WPT)系统是一种开关系统,其大信号模型是研究系统运行特性和稳定性的基础。建模的关键是如何描述系统中的非线性、离散开关变量,为解决这一问题,该文提出一种基于S型激活函数的建模方法。S型激活函数是连续、平滑、可微的且在一定值时具有饱和特性,因此可利用陡度因子较大的激活函数来近似开关的切换过程,将WPT系统由离散的开关系统转变为连续系统。该文以LCC-S型WPT系统为研究对象,构建其开环和闭环模式下激活函数模型,利用该模型分析控制器参数和系统参数对瞬态行为和稳定性的影响,并通过仿真和实验进行验证。结果表明,所构建的模型与仿真和实验结果吻合较好。该模型数学表达式结构简单统一,物理意义明确,是一个具有普遍意义的高精度大信号连续模型。关键词:无线电能传输系统LCC-S补偿激活函数大信号模型稳定性中图分类号:TM7240引言无线电能传输[1-3](WirelessPowerTransfer,WPT)系统根据电路运行特性,可以将一个开关周期分为不同的开关状态,在每个开关状态下,对应一个由连续状态变量表示的子系统,因此WPT系统可以被视为由离散开关状态和连续状态变量组成的开关系统,开关器件在每个连续子系统中有选择地保持某一固定开关状态,以满足系统动态响应的要求。建模的关键是描述离散开关变量和连续状态变量之间的相互作用并建立统一的模型[4]。状态空间平均法[5]使用状态变量在一个开关周期的平均值建立模型,只保留状态变量的低频成分,忽略其高频纹波分量,从而建立一个连续的系统模型。然而,由于在稳态运行时LCC-S型WPT系统[6-7]中各电量是交流量,对其进行状态空间平均将丢失其最主要的波形信息,因此不能使用状态空间平均法进行建模。为此,研究学者提出了广义状态空间平均(GeneralizedState-SpaceAveraging,GSSA)法[8-9]、扩展描述函数(ExtendedDescribingFunction,EDF)法[10]、耦合模理论[11]及离散迭代模型[12]等方法来解决WPT系统的建模问题。广义状态空间法和描述函数法都实现了从非线性时变不连续的状态空间方程到线性时不变连续状态空间方程,甚至局部线性化方程的转换。相比较而...