基于神经网络的配气站运行参数智能控制模型研究_卢万.pdf

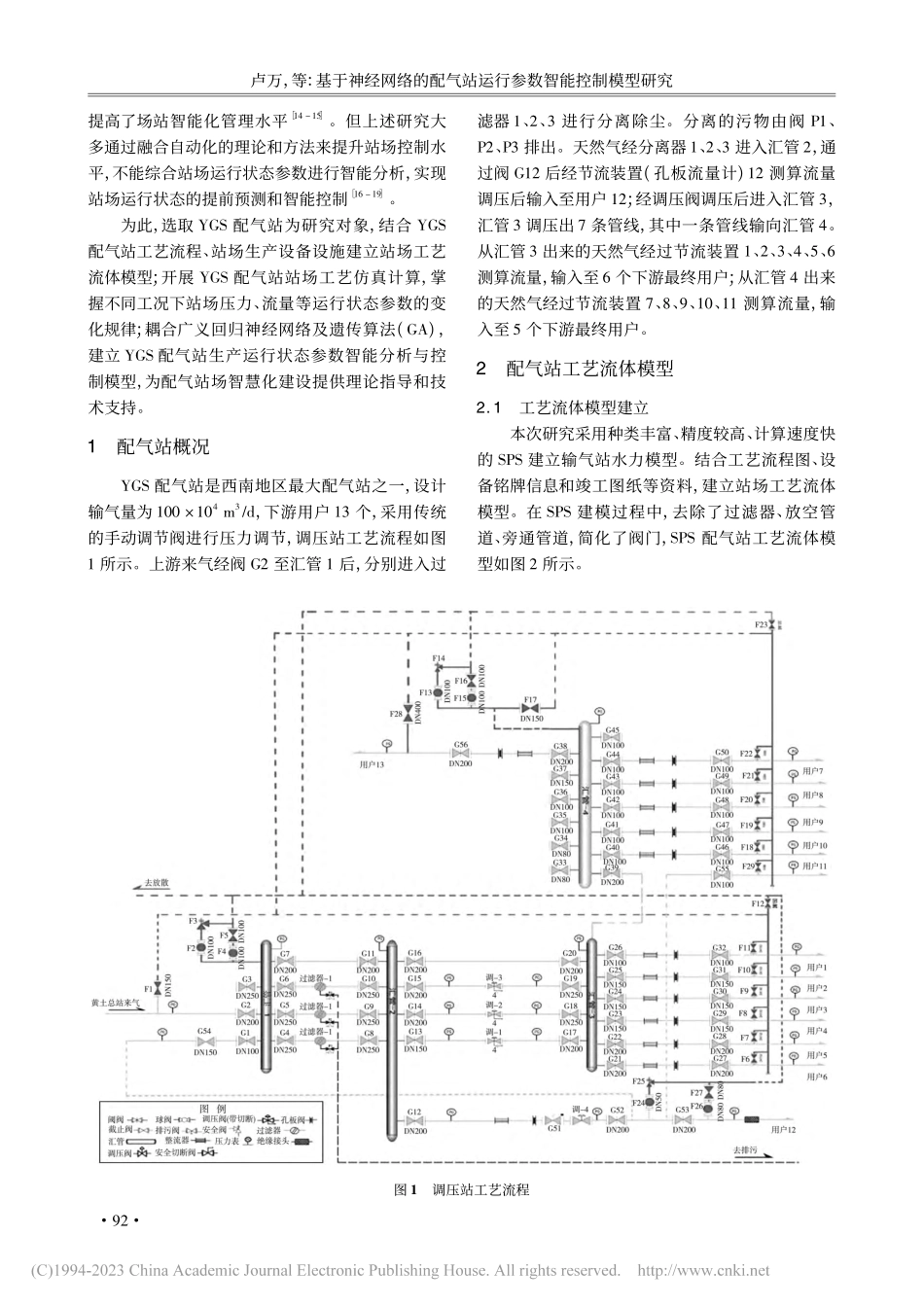
第 25 卷 第 1 期重庆科技学院学报(自然科学版)2023 年 2 月基于神经网络的配气站运行参数智能控制模型研究卢 万1王 飞2黎登辉1张瀚月1梁 平3游书婷3，4黄辉荣3(1 中国石油西南油气田燃气分公司，成都 610017;2 中国石油西南油气田公司，成都 610017;3 重庆科技学院 石油与天然气工程学院，重庆 401331;4 中国石油化工股份有限公司 西南油气分公司采气四厂，成都 610017)收稿日期:2022 05 02基金项目:重庆市自然科学基金项目“纳米杂化降凝剂 NPPD 对含蜡油体系表观流变特性的改善机理研究”(CSTC2021JCYJ MSXMX0918);重庆市教委科技研究计划项目“纳米降凝剂 NPPD 对含蜡油蜡沉积特性的影响机理研究”(KJQN202101545);重庆科技学院科研启动项目“新型纳米流动改性剂 NFM 对含蜡油微观结晶过程的调控机理研究”(CKC2021003)作者简介:卢万(1992 )，男，在读硕士研究生，工程师，研究方向为油气田开发、燃气管道管理。通信作者:黄辉荣(1992 )，男，博士，讲师，研究方向为油气田地面集输技术、油气管道长距离输送技术、油气管道及站场智能化。摘要:人工智能、大数据等新兴技术的发展极大地推动了油气行业的智能化升级改造，但目前部分配气站仍采用传统的人工干预进行调节，存在控制滞后、自适应能力差等问题，严重威胁着下游用户的用气安全。为此，以 YGS 配气站为研究对象，建立了站场运行状态参数智能分析与控制模型，获得了正常和异常工况下配气站运行状态参数的变化规律，形成了配气站智能控制方法。研究结果表明，站场仿真模型获得的流量、出站压力等参数与实际运行数据吻合较好;配气站运行参数智能控制模型实现了对不同工况下站场运行状态参数的准确控制，为配气站智慧化建设奠定了基础。关键词:配气站;工艺流体模型;智能算法;控制模型中图分类号:TP183文献标识码:A文章编号:1673 1980(2023)01 0091 080前言智慧输配气站是现代天然气输配智能化调控的重要发展方向，也是未来大型管网智慧管理的基础1 2。传统输配气站的 SCADA 系统注重站点运行状况的数据采集，包括压力、温度、流量等数据的采集和报警，对站场控制的关注较少3 5。当遭遇特殊工况时，配气站存在自适应能力差、控制精度低等问题6 7。加快配气站智能化建设是保证站场运行安全的关键8。目前，学者们在配气站智能化建设方面开展了大量的研究9。顾亚雄等人提出了一种基于模糊控制规则的 PID 控制方法，通过调整比例、积分、微分等 3 个参数来提高配气站调压系统的响应速度和抗干扰性能10。李立刚等人采用改进的隐式广义预测控制方法进行压力控制，通过设定最小阀门来控制增量初始值，改善阀门死区问题11。周湃等人提出首先根据站场上下游用户的用气规律，合理预测站场出入口压力的变化趋势;然后设定合适的阀门开度，以避免流量超过设定值或供气量不足12。吴悠等人利用管道压力控制实验平台进行黄金分割自适应控制实验，实验结果表明，黄金分割自适应控制的精度高、现场调试简单、控制方案优越13。梁怿、王树祺等人提出了基于无人化智能调压控制逻辑系统的自适应广义预测算法，解决了输气场站天然气超输、调压不稳定、调压中断等问题，19DOI:10.19406/ki.cqkjxyxbzkb.2023.01.003卢万，等:基于神经网络的配气站运行参数智能控制模型研究提高了场站智能化管理水平14 15。但上述研究大多通过融合自动化的理论和方法来提升站场控制水平，不能综合站场运行状态参数进行智能分析，实现站场运行状态的提前预测和智能控制16 19。为此，选取 YGS 配气站为研究对象，结合 YGS配气站工艺流程、站场生产设备设施建立站场工艺流体模型;开展 YGS 配气站站场工艺仿真计算，掌握不同工况下站场压力、流量等运行状态参数的变化规律;耦合广义回归神经网络及遗传算法(GA)，建立 YGS 配气站生产运行状态参数智能分析与控制模型，为配气站场智慧化建设提供理论指导和技术支持。1配气站概况YGS 配气站是西南地区最大配气站之一，设计输气量为 100 104m3/d，下游用户 13 个，采用传统的手动调节阀进行压力调节，调压站工艺流程如图1 所示。上游来气经阀 G2 至汇管 1 后，分别进入过滤器 1、2、3 进行分离除尘。分离的污物由阀 P1、P2、P3 排出。天然气经分离器 1、2、3 进入汇管 2，通过阀 G12 后经节流装置(孔板流量计)12 测算流量调压后输入至用户 12;经调压阀调压后进入汇管 3，汇管 3 调压出 7 条管线，其中一条管线输向汇管 4。从汇管 3 出来的天然气经过节流装置 1、2、3、4、5、6测算流量，输入至 6 个下游最终用户;从汇管 4 出来的天然气经过节流装置 7、8、9、10、11 测算流量，输入至 5 个下游最终用户。2配气站工艺流体模型21工艺流体模型建立本次研究采用种类丰富、精度较高、计算速度快的 SPS 建立输气站水力模型。结合工艺流程图、设备铭牌信息和竣工图纸等资料，建立站场工艺流体模型。在 SPS 建模过程中，去除了过滤器、放空管道、旁通管道，简化了阀门，SPS 配气站工艺流体模型如图 2 所示。图 1调压站工艺流程29卢万，等:基于神经网络的配气站运行参数智能控制模型研究图 2SPS 配气站工艺流体模型摩阻系数 是计算摩阻损失的关键参数之一。对比不同摩阻系数计算公式的适用条件，本次研究选取 Colebrook 公式进行管道仿真计算20，如式(1)式(4)所示:hf=LDv22g(1)hj=v22g(2)=f(e，D)(3)1=2lg(3 7D+2 51e)(4)式中:hf 沿程摩阻损失，m;管道摩阻系数;L 管道长度，m;D 管道内径，m;v 流体在管道内的平均流速，m/s;g 重力加速度，m/s2;hj 局部摩阻损失，m;局部损失(阻力)系数，其大小与局部障碍物的结构形式有关，通过实验确定;e 雷诺数;绝对粗糙度，m。调节阀是一个局部阻力可变的节流元件，通过改变阀芯行程来改变局部阻力系数，其关键参数为压力恢复系数、临界压差比和管件修正系数。对于给定的调节阀，压力恢复系数是一个固定常数，其值与阀的结构、流路形式有关，与阀门口径大小无关;临界压差比只取决于调节阀结构，即流路形式;管件修正系数与调节阀的公称直径、管道直径有关。结合站场实际生产情况，采用非阻塞流的流量系数法计算阀门压降损失，如式(5)所示:Cn=Qg5 19p1YT1gZX(5)式中:Cn 阀门压降损失;Qg 标准气体体积流量，m3/h;p1 阀前绝对压力，kPa;Y 膨胀系数;T1 阀入口处流体温度，;g 气体密度，kg/m3;Z 气体压缩系数;X 压差比。22工艺流体模型验证基于站场工艺流体模型，结合 SCADA 采集的生产运行数据对站内摩阻进行修正，以验证配气站工艺流体模型的准确性。2 2 1配气站运行状态参数分析根据天然气调压站实际运行数据，通过 SCADA系统以 1 min 的采样间隔连续采集现场 13 个孔板流量计(其中用户 5、7、9 为预留用户)，以及与工艺流程导通相关的阀数据、调节阀阀位数据，共采集到1 051 200 组数据。以 2020 年 3 月 1 日 2020 年3 月 7 日用气量为例(见图 3)，配气站下游各用户用气量在一定时间的周期内出现了剧烈波动。结合现场调研发现，配气站定期校时补气、清洗补气、异39卢万，等:基于神经网络的配气站运行参数智能控制模型研究常退出补气是造成用气量出现波动的主要原因。为验证模型的有效性，剔除用户校时补气、清洗补气等时段的数据(见图 4)。用户 3 的用气量呈先平稳，后逐渐增加，最后趋于稳定的状态;用户 11 的用气量呈周期性变化;用户 10 基本处于停输状态;用户12 的用气高峰出现在最后 2 日;其余用户的用气量基本保持平稳。图 3整理前的用户用气量图 4整理后的用户用气量2 2 2工艺流体模型验证以 YGS 配气站气体进站压力、压力调节阀开度和截断阀开关状态作为模型输入，以用户出站压力、用气量作为模型输出，进行站场工艺流程仿真计算。以 2020 年 3 月 2 日 3 日为例，分别对用户 1、用户 12 进行仿真计算，结果如图 5、图 6 所示。图 5用户 1 的压力、流量仿真结果由图 5、图 6 可知，上游来气量和下游用户用气量的变化是不可预见的，各用户白天的供气压力出现下降、平稳、上升的状态，晚上供气压力基本处于平缓波动的状态。用户 1 晚上的用气量均呈先缓慢49卢万，等:基于神经网络的配气站运行参数智能控制模型研究图 6用户 12 的压力、流量仿真结果变化，之后趋于平稳的状态;用户 12 的用气量呈小幅度波动状态。与站场实际运行数据进行对比发现，经 SPS 模拟得到的出站压力、流量与现场数据的误差小于5%，说明站场工艺流体模型具有较高的准确性，为站场运行状态参数的智能控制奠定了基础。3智能控制模型研究对于多用户类型的配气站，站内各参数之间的关系复杂，采用传统的数值方法难以构建准确的数学模型。天然气配气站关注的重点是下游用户用气量，并非全站各点的水热力参数值。因此，本次研究基于广义回归神经网络算法，建立站场智能控制模型，以实现站场运行状态参数的智能控制。31控制基础理论广义回归神经网络(generalized regression neuralnetwork，GNN)由 Specht 于 1991 年提出，是径向基神经 网 络(radical basis function neural network，BFNN)的一种，具有很强的非线性拟合能力和学习速度、高容错性和高鲁棒性。基于此，本次研究采用 GNN 来建立站场智能控制模型。GNN 结构由输入层、模式层、求和层和输出层构成，如图 7 所示。图 7GNN 结构神经元 i 的输出为输入变量与其对应样本 X 之间 Euclid 距离平方的指数平方的指数形式，即 D2i=(X Xi)T(X Xi)。其中，X 为输入变量;Xi为第 i个神经元对应的学习样本。输入层的节点数等于样本特征维度，则模式层的传递函数如式(6)所示:pi=exp(X Xi)T(X Xi)22(6)式中:pi 模式层第 i 个神经元的训练结果，i=1，2，n;光滑因子。59卢万，等:基于神经网络的配气站运行参数智能控制模型研究使用 2 种类型的神经元在求和层中求和。一种是将所有模式层神经元的输出进行算术求和，模式层与各神经元的连接权值为 l，其传递函数如式(7)所示:SD=ni=1exp(X Xi)T(X Xi)22(7)另一种是将所有模式层神经元的输出进行加权求和，模式层中第 i 个神经元与求和层中第 j 个分子求和，神经元之间的连接权值为第 i 个输出样本的第 j 个元素，其传递函数如式(8)所示:SN=ni=1yijexp(X Xi)T(X Xi)22(8)输出层中的神经元数目等于学习样本中输出向量的维数 k，各神经元将求和层的输出相除，则神经元 j 的输出对应估计结果为 y 的第 j 个元素。输出层的传递函数如式(9)所示:yj=SDSN，j=1，2，k(9)传统 GNN 模型的预测精度主要取决于光滑因子的选取，在样本数据较少时也有较好的预测效果。但若光滑因子选取不合理，就会导致神经网络预测误差增大。因此，本次研究采用 GNN 改进算法(GA GNN)，利用 GA 替代 GNN 训练过程，对 进行优化。采用交叉验证的方法对样本进行随机分组，基于 GA 构建适应度函数，如式(10)所示:E()=1mmiy(xi)y(xi)(10)式中:E()当前光滑因子下测试样本的误差均值;m 测试样本数;y(xi)测试样本的预测值;y(xi)测试样本的实际值。令种群大小为 10，交叉概率为 0 1，变异概率为 0 1，最大迭代次数为 10。以均方根误差(MSE)作为预测精度的衡量指标，如式(11)所示:EMS=1NNi=1(yi yi)2(11)