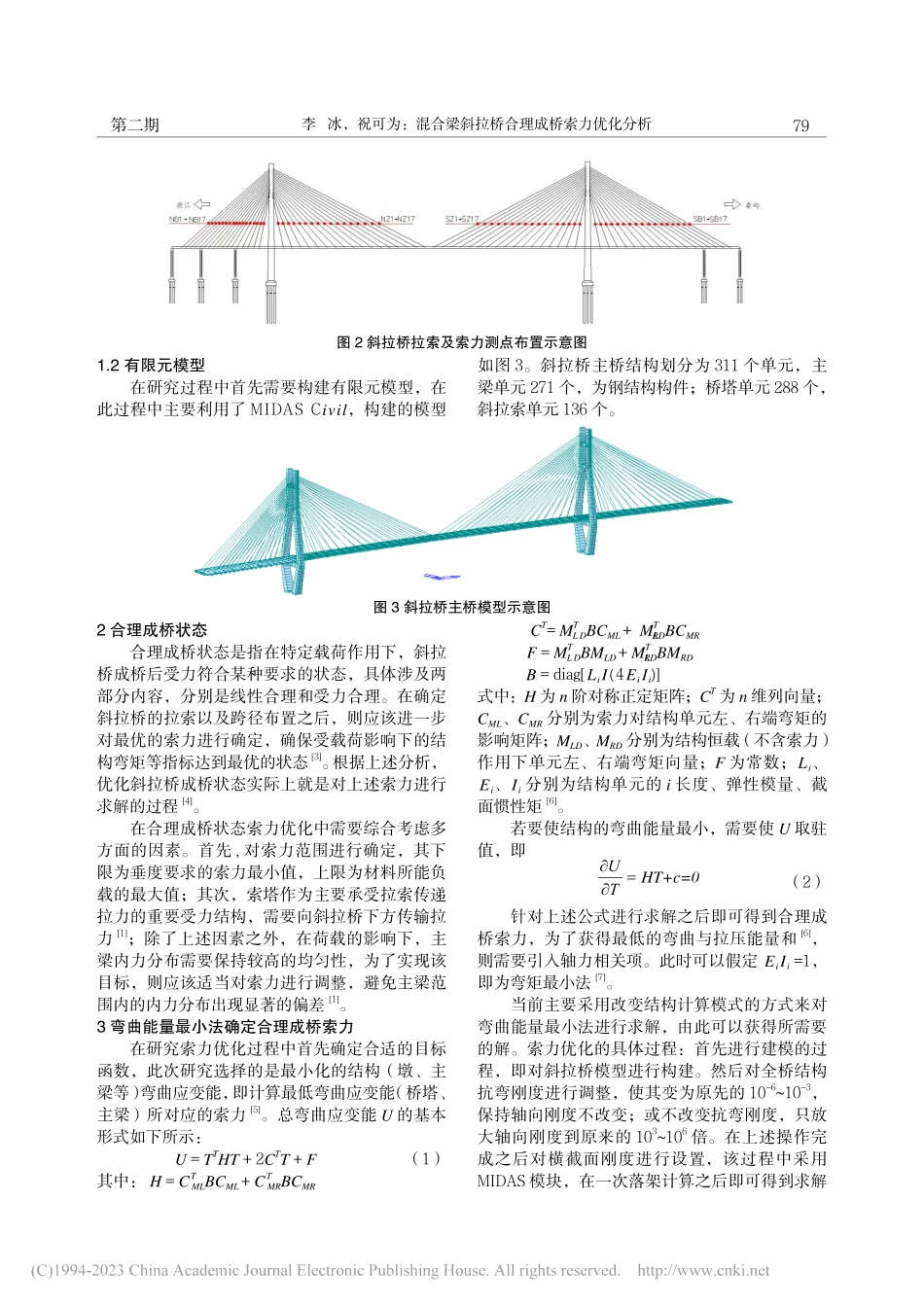
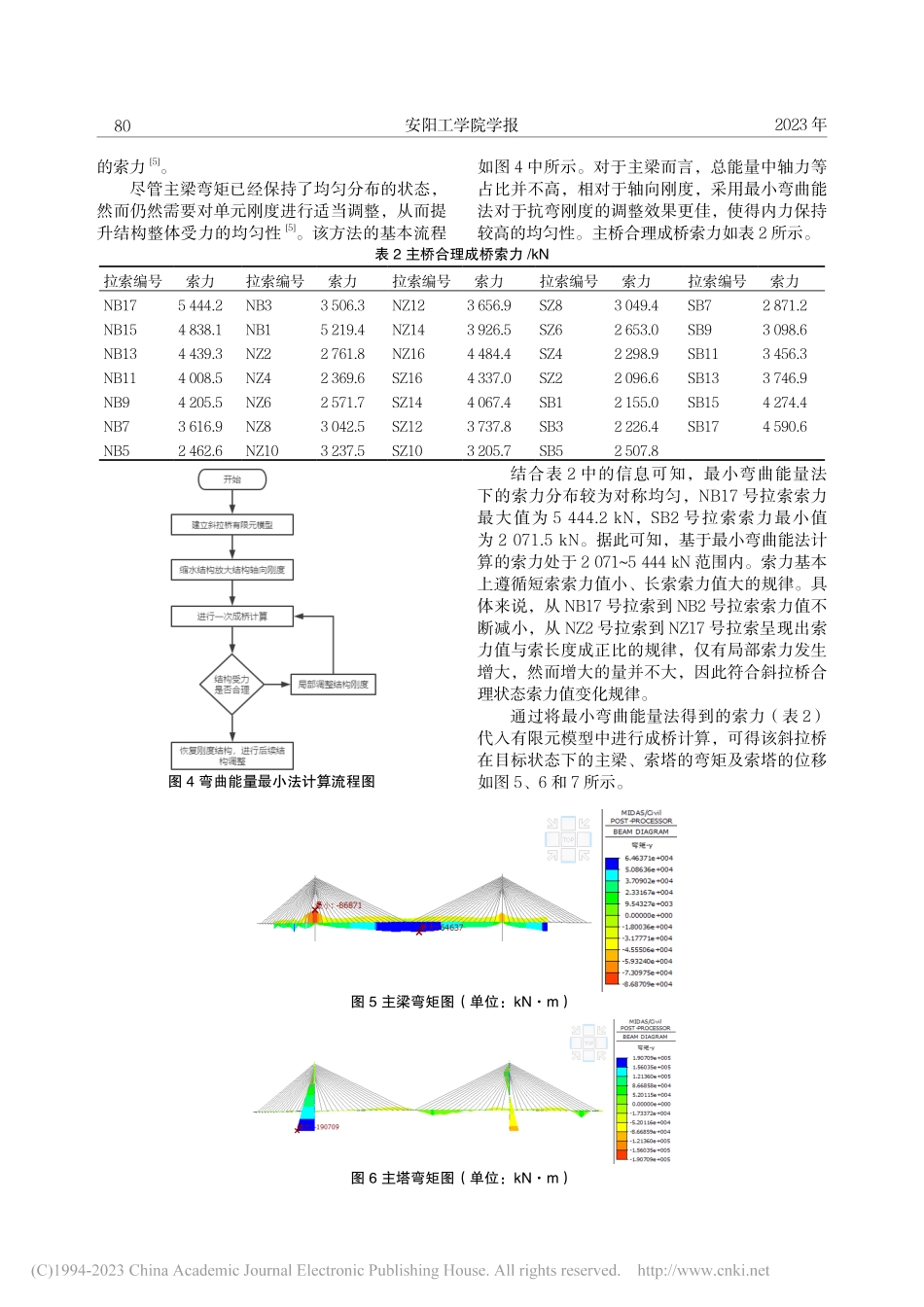
安阳工学院学报JournalofAnyangInstituteofTechnologyVol.22No.2(Gen.No.122)Mar.,2023第22卷第2期(总第122期)2023年3月DOI:10.19329/j.cnki.1673-2928.2023.02.015混合梁斜拉桥合理成桥索力优化分析李冰,祝可为(福建船政交通职业学院土木工程学院,福州350007)摘要:针对混合梁斜拉桥合理成桥索力开展优化研究,结合改进的最小弯曲能量法对半漂浮体系单侧不对称混合梁斜拉桥合理成桥状态进行确定,通过模拟获得了在成桥状态时的索力值。最终得到的结果显示:实测结果与计算结果保持了较高的一致性,满足了规范的相关要求。本研究将为类似工程参数的设计与优化提供必要的基础数据。关键词:混合梁斜拉桥;索力;有限元分析;最小弯曲能量法;实测索力中图分类号:U491文献标志码:A文章编号:1673-2928(2023)02-0078-05斜拉桥是由主梁、拉索、索塔组成的一种组合体系桥梁,它通过斜拉索张拉在斜拉桥塔、梁之间,改变全桥的受力状态,由此形成典型的高次超静定结构。在整个结构中,斜拉索属于关键的部分,能够将纵向支承提供给主梁,继而实现对其弯矩的有效控制,保证整体结构的稳定性。因此拉索索力成为影响斜拉桥受力的一个核心因素,必须对其进行科学分析与设计。在设计中通过斜拉索的调整来改变结构的受力分配,确保主梁应力适宜。而在斜拉桥设计过程中应该借助于模拟方法来确定最优的索力,使得斜拉桥处于最佳的受力状态[1]。在本研究中针对斜拉桥受力状态进行分析,并结合某斜拉桥开展实例分析,对其成桥索力进行分析和计算,在此基础上确定合理的索力。在研究过程中利用MIDASCivil工具,最终发现计算的结果和测量的结果是吻合的,实测索力与计算索力误差较小,符合工程规范要求。本研究具有一定的实用价值,能够为同类工程提供必要的基础数据。1工程概况及模型建立1.1工程概况某斜拉桥主桥采用半漂浮体系单侧不对称混合梁结构;主桥跨径为(49+58+61)m+535m+(198+60)m。边跨北侧边跨内设置2个辅助墩,南侧边跨设1个辅助墩,主桥全长961m[2];桥型布置图如图1。主桥为主跨535m单侧混合梁斜拉桥(南边跨、中跨、北边跨依次是钢箱梁、钢箱梁、混凝土梁),南、北索塔总高分别是192.2m、189.4m。各个部分采用的混凝土结构是不同的,其中采用预应力混凝土结构的包括上塔柱斜拉索锚固区以及索塔横梁,其他塔柱部分为普通混凝土结构。全桥共有136根斜拉索,具体布置如图2所示,测点编号左右幅采用L\R区分。材料具体设计参数见表1。表1主...