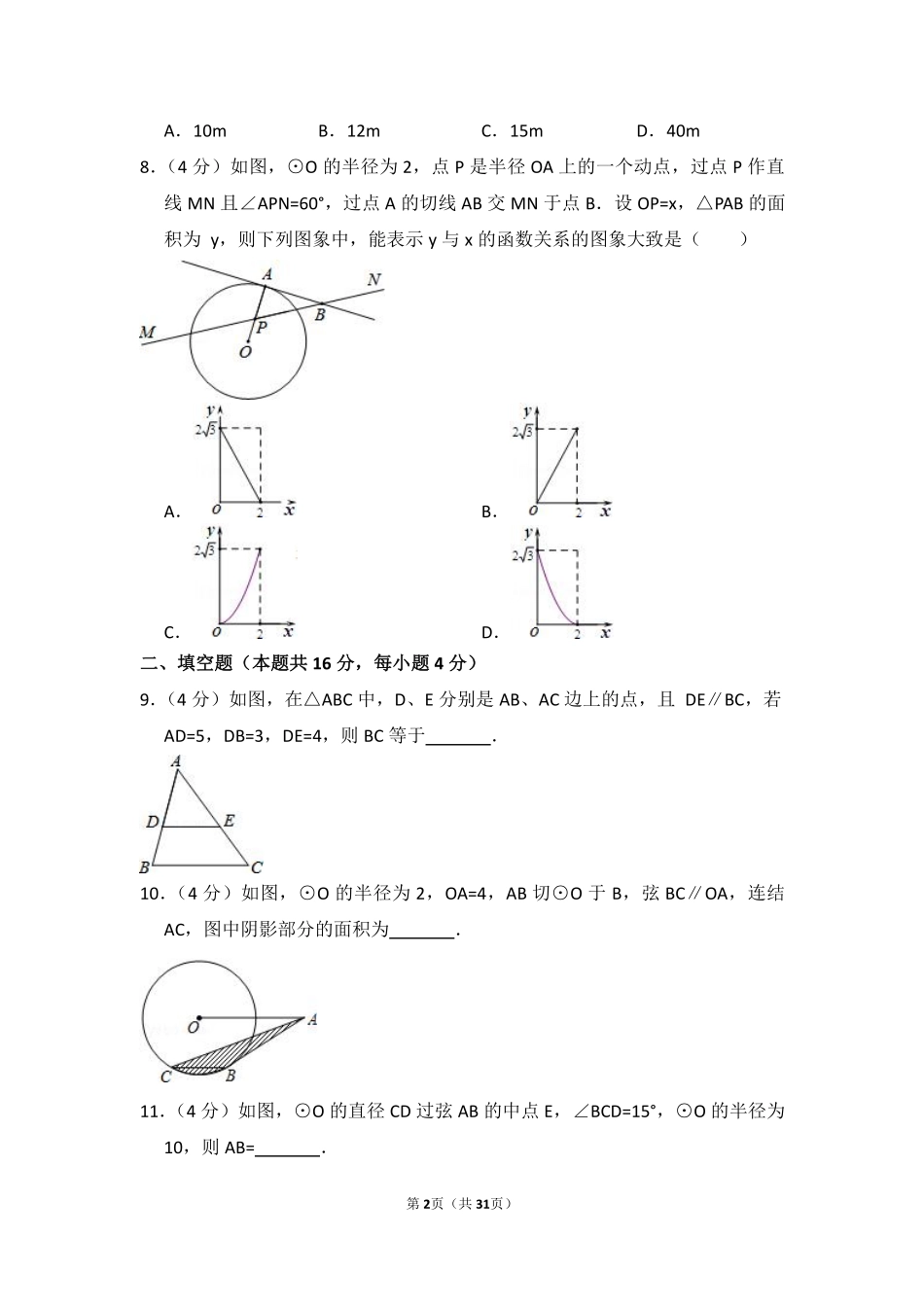
第1页(共31页)2014-2015学年北京市房山区九年级(上)期末数学试卷一、选择题(本题共32分,每小题4分)下列各题均有四个选项,其中有且只有一个是符合题意的.请将正确选项前的字母填在下表中相应的位置上.1.(4分)二次函数y=﹣(x﹣2)2+5图象的顶点坐标是()A.(﹣2,5)B.(2,5)C.(﹣2,﹣5)D.(2,﹣5)2.(4分)如图,⊙O是△ABC的外接圆,若AB=OA=OB,则∠C等于()A.30°B.40°C.60°D.80°3.(4分)在△ABC中,∠C=90°,AC=8,BC=6,则sinB的值是()A.B.C.D.4.(4分)已知点P(﹣3,2)是反比例函数的图象上一点,则此反比例函数的解析式是()A.B.C.D.5.(4分)若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为()A.1:2B.2:1C.1:4D.4:16.(4分)如图,弦AB⊥OC,垂足为点C,连接OA,若OC=2,AB=4,则OA等于()A.2B.2C.3D.27.(4分)在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为()第2页(共31页)A.10mB.12mC.15mD.40m8.(4分)如图,⊙O的半径为2,点P是半径OA上的一个动点,过点P作直线MN且∠APN=60°,过点A的切线AB交MN于点B.设OP=x,△PAB的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是()A.B.C.D.二、填空题(本题共16分,每小题4分)9.(4分)如图,在△ABC中,D、E分别是AB、AC边上的点,且DE∥BC,若AD=5,DB=3,DE=4,则BC等于.10.(4分)如图,⊙O的半径为2,OA=4,AB切⊙O于B,弦BC∥OA,连结AC,图中阴影部分的面积为.11.(4分)如图,⊙O的直径CD过弦AB的中点E,∠BCD=15°,⊙O的半径为10,则AB=.第3页(共31页)12.(4分)抛物线y=x2﹣x+(其中n是正整数)与x轴交于An、Bn两点,若以AnBn表示这两点间的距离,则A1B1=;A1B1+A2B2=;A1B1+A2B2+A3B3+…+AnBn=.(用含n的代数式表示)二、解答题(本题共30分,每小题5分)13.(5分)计算:(﹣1)0﹣2cos30°﹣()﹣1+.14.(5分)如图,C为线段BD上一点,AC⊥CE,AB⊥BD,ED⊥BD.求证:=.15.(5分)已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,求k的取值范围.16.(5分)如图,在△ABC中,∠C=90°,sinA=,D为AC上一点,∠BDC=45°,DC=6,求AB的长.17.(5分)小红想要测量校园内一座教学楼CD的高度.她先在A处测得楼顶C的仰角α=30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角β=60°...