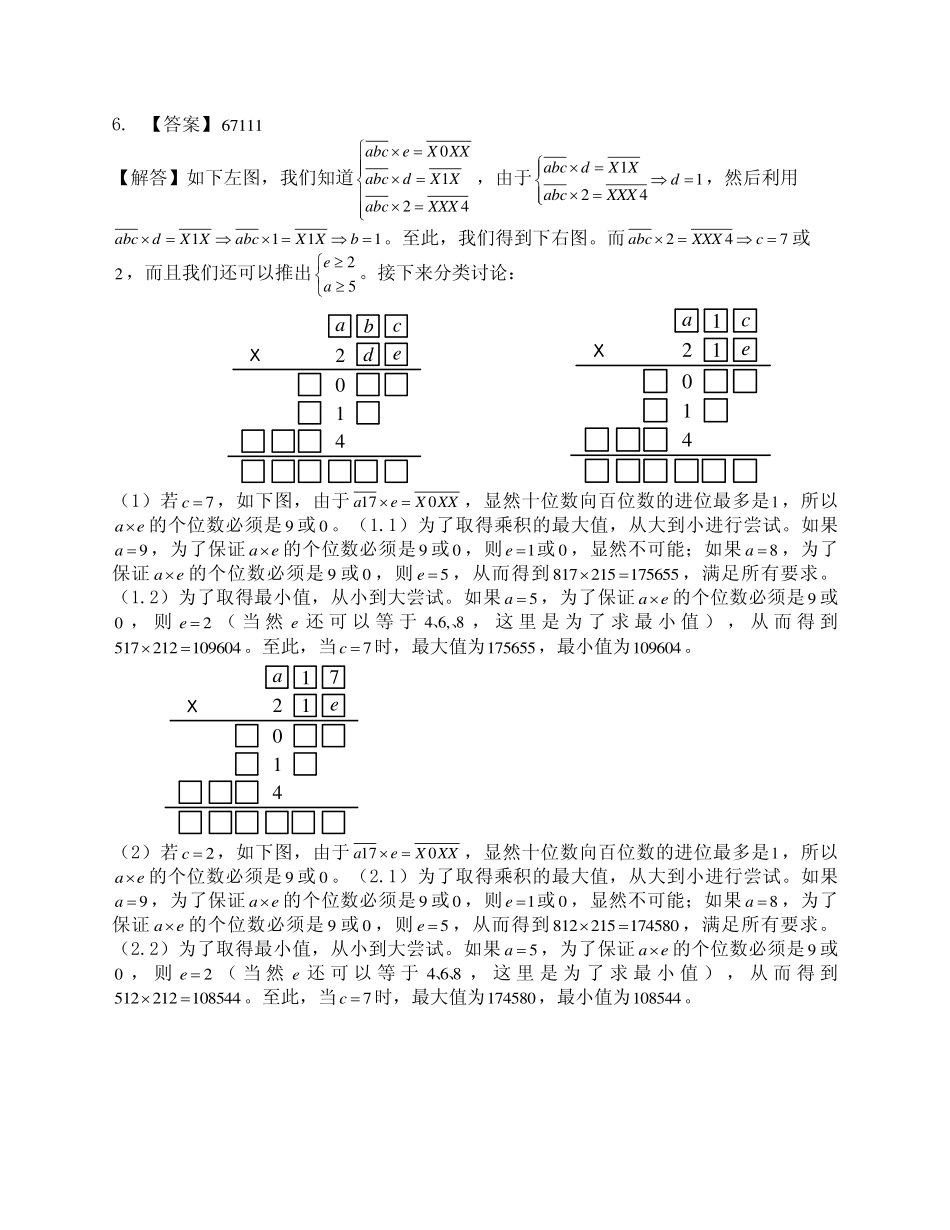
第14届“中环杯”中小学生思维能力训练活动五年级决赛答案一、填空题:1.【答案】1203【解答】11.99731.0929711.99731.09112711.997311.99271199,而2211318422,所以和为119941203。2.【答案】11【解答】4204mod138148mod1316164mod13,所以42081416164841683811mod13。3.【答案】45【解答】设甲班原有5k个人,则乙班原有7k个人。根据题意,列出方程5349735kkk。所以甲班原有学生545k人。4.【答案】50【解答】显然,9|96642891405mod911|96642891405mod11ABABABAB。考虑到ABAB、同奇偶,所以可能的方程组有5550ABAABB或144610ABABAB。由于9B,所以只有一种可能,所以50AB。5.【答案】400【解答】联结EF。由于33ABAEEFACAF//BC,所以1FBDEBDSSS,所以122403EBDEDCEBCABCSSSSSS,为一个定值。显然,当1220SS时,12SS最大为400。OFEABCD6.【答案】67111【解答】如下左图,我们知道0124abceXXXabcdXXabcXXX,由于1124abcdXXdabcXXX,然后利用1111abcdXXabcXXb。至此,我们得到下右图。而247abcXXXc或2,而且我们还可以推出25ea。接下来分类讨论:edcba4102e1c1a4102(1)若7c,如下图,由于170aeXXX,显然十位数向百位数的进位最多是1,所以ae的个位数必须是9或0。(1.1)为了取得乘积的最大值,从大到小进行尝试。如果9a,为了保证ae的个位数必须是9或0,则1e或0,显然不可能;如果8a,为了保证ae的个位数必须是9或0,则5e,从而得到817215175655,满足所有要求。(1.2)为了取得最小值,从小到大尝试。如果5a,为了保证ae的个位数必须是9或0,则2e(当然e还可以等于46,8、、,这里是为了求最小值),从而得到517212109604。至此,当7c时,最大值为175655,最小值为109604。e171a4102(2)若2c,如下图,由于170aeXXX,显然十位数向百位数的进位最多是1,所以ae的个位数必须是9或0。(2.1)为了取得乘积的最大值,从大到小进行尝试。如果9a,为了保证ae的个位数必须是9或0,则1e或0,显然不可能;如果8a,为了保证ae的个位数必须是9或0,则5e...