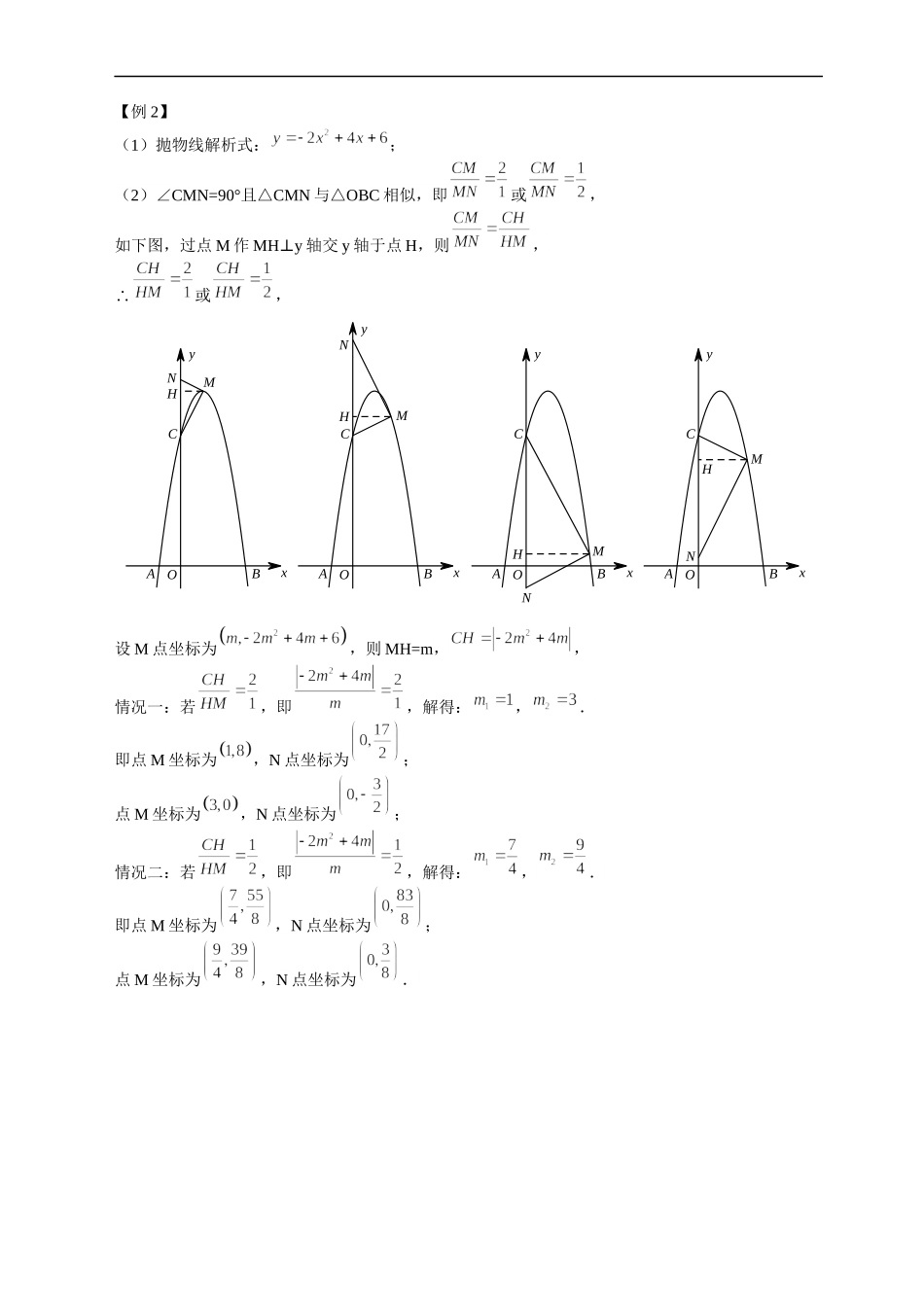
【例1】(1)直线解析式:;点B坐标为;(2)分类讨论:①∠BAC=90°;②∠ABC=90°(图太大不画了);③∠ACB=90°(两个)CMNMNCxyOABBAyx构造三垂直相似,可得:当∠BAC=90°时,可得点坐标为;当∠ABC=90°时,可得点坐标为;当∠ACB=90°时,可得点坐标为、点坐标为.(3)过点M作MNMP⊥交AB于点Q,则,即,QxyOABNMP设点M坐标为,则点Q坐标为,又点N坐标为,∴,,∴,当m=6时,取到最大值18.【例2】(1)抛物线解析式:;(2)∠CMN=90°且△CMN与△OBC相似,即或,如下图,过点M作MHy⊥轴交y轴于点H,则,∴或,MNHOABCxyMNHOABCxyMNHyOABCxHMNyxCBAO设M点坐标为,则MH=m,,情况一:若,即,解得:,.即点M坐标为,N点坐标为;点M坐标为,N点坐标为;情况二:若,即,解得:,.即点M坐标为,N点坐标为;点M坐标为,N点坐标为.【例3】(1)解析式:;(2)题目要求恰好有2个P点,且是求m的值,所以一定是个特殊位置.考虑到∠DCP=∠FOP,故有两种对应关系:①若△DCP∽△FOP,无论m为何值,有且仅有一个这样的P点使得△DCP∽△FOP.②若△DCP∽△POF,不难求得∠DPF=90°,作辅助圆:连接DF,以DF为直径作圆,当圆与线段OC相离时,P点个数为0;当圆与线段OC相切时,P点个数为1;当圆与线段OC相交时,P点个数为2.∴圆与线段相切的时候,有且仅有一个P点,使得△DCP∽△POF.EFyxPODC由题意得:C(0,1+m),故D(2,1+m),又F(1,0),可得DF中点E点坐标为,由圆E与y轴相切,得:EP=EF,即,解得:,(舍),故m的值为,若△DCP∽△FOP,P点坐标为,若△DCP∽△POF,P点坐标为.但是,若圆E与y轴相交,且其中一个交点与①中的点是同一点,则同样满足恰有2个P点,使得△PCD与△POF相似,即此P点既满足△DCP∽△FOP,也满足△DCP∽△POF,△DCP与△POF均为等腰直角三角形.OP=OF=1,PC=CD=2,故m的值为2,若△DCP∽△FOP,P点坐标为(0,1),若△DCP∽△POF,P点坐标为(0,2).FyxPODCCDOPxyF综上所述,m的值为时,对应的P点坐标为或;m的值为2时,对应的P点坐标为(0,1)或(0,2).