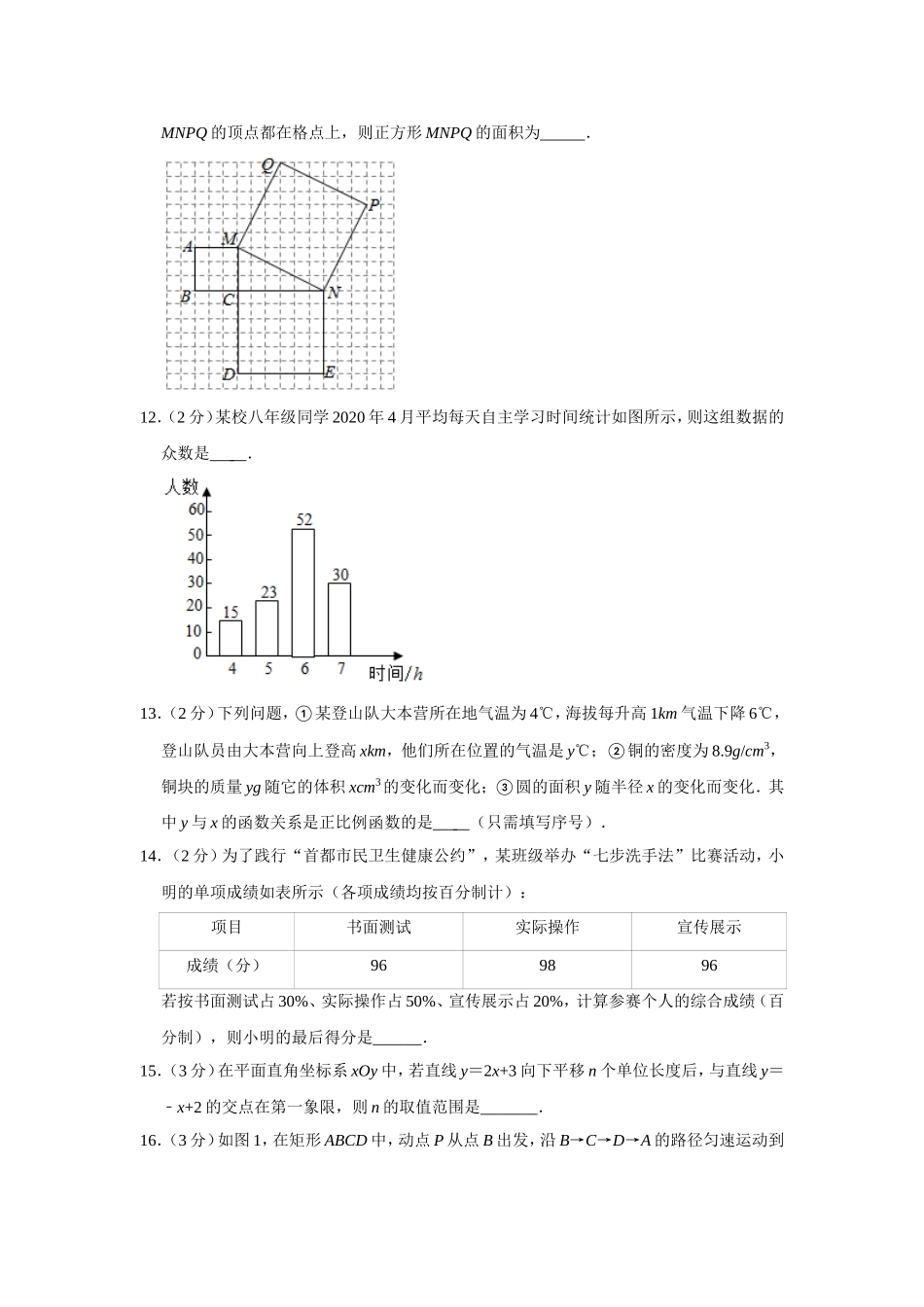
2019-2020学年北京市朝阳区八年级(下)期末数学试卷(选用)一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.(2分)若二次根式有意义,则实数x的取值范围是()A.x≠8B.x≥8C.x≤8D.x=82.(2分)满足下列关系的三条线段a,b,c组成的三角形一定是直角三角形的是()A.a<b+cB.a>b﹣cC.a=b=cD.a2=b2﹣c23.(2分)若菱形的两条对角线的长分别为6和10,则菱形的面积为()A.60B.30C.24D.154.(2分)下列曲线中,表示y是x的函数的是()A.B.C.D.5.(2分)《九章算术》内容丰富,与实际生活联系紧密,在书上讲述了这样一个问题“今有垣高一丈,倚木于垣,上与垣齐.引木却行一尺,其木至地.问木长几何?”其内容可以表述为:“有一面墙,高一丈.将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆上端恰好沿着墙滑落到地面上.问木杆长多少尺?”(说明:1丈=10尺)设木杆长x尺,依题意,下列方程正确的是()A.x2=(x﹣1)2+102B.(x+1)2=x2+102C.x2=(x﹣1)2+12D.(x+1)2=x2+126.(2分)如图,矩形ABCD的对角线AC,BD相交于点O,AB=2,∠ABO=60°,线段EF绕点O转动,与AD,BC分别相交于点E,F,当∠AOE=60°时,EF的长为()A.1B.C.2D.47.(2分)想要计算一组数据:197,202,200,201,199,198,203的方差s2,在计算平均数的过程中,将这组数据的每一个数都减去200,得到一组新数据﹣3,2,0,1,﹣1,﹣2,3,且新的这组数据的方差为4,则s2为()A.4B.16C.196D.2048.(2分)已知O为数轴原点,如图,(1)在数轴上截取线段OA=2;(2)过点A作直线n垂直于OA;(3)在直线n上截取线段AB=3;(4)以O为圆心,OB的长为半径作弧,交数轴于点C.根据以上作图过程及所作图形,有如下四个结论:①OC=5;②OB=;③3<OC<4;④AC=1.上述结论中,所有正确结论的序号是()A.①②B.①③C.②③D.②④二、填空题(本题共18分,第9-14题,每小题2分,第15-16题,每小题2分)9.(2分)已知x=+,y=﹣,则xy=.10.(2分)下列命题,①对顶角相等;②两直线平行,同位角相等;③平行四边形的对角相等.其中逆命题是真命题的命题共有个.11.(2分)如图所示的正方形网格中,每个小正方形的面积均为1,正方形ABCM,CDEN,MNPQ的顶点都在格点上,则正方形MNPQ的面积为.12.(2...