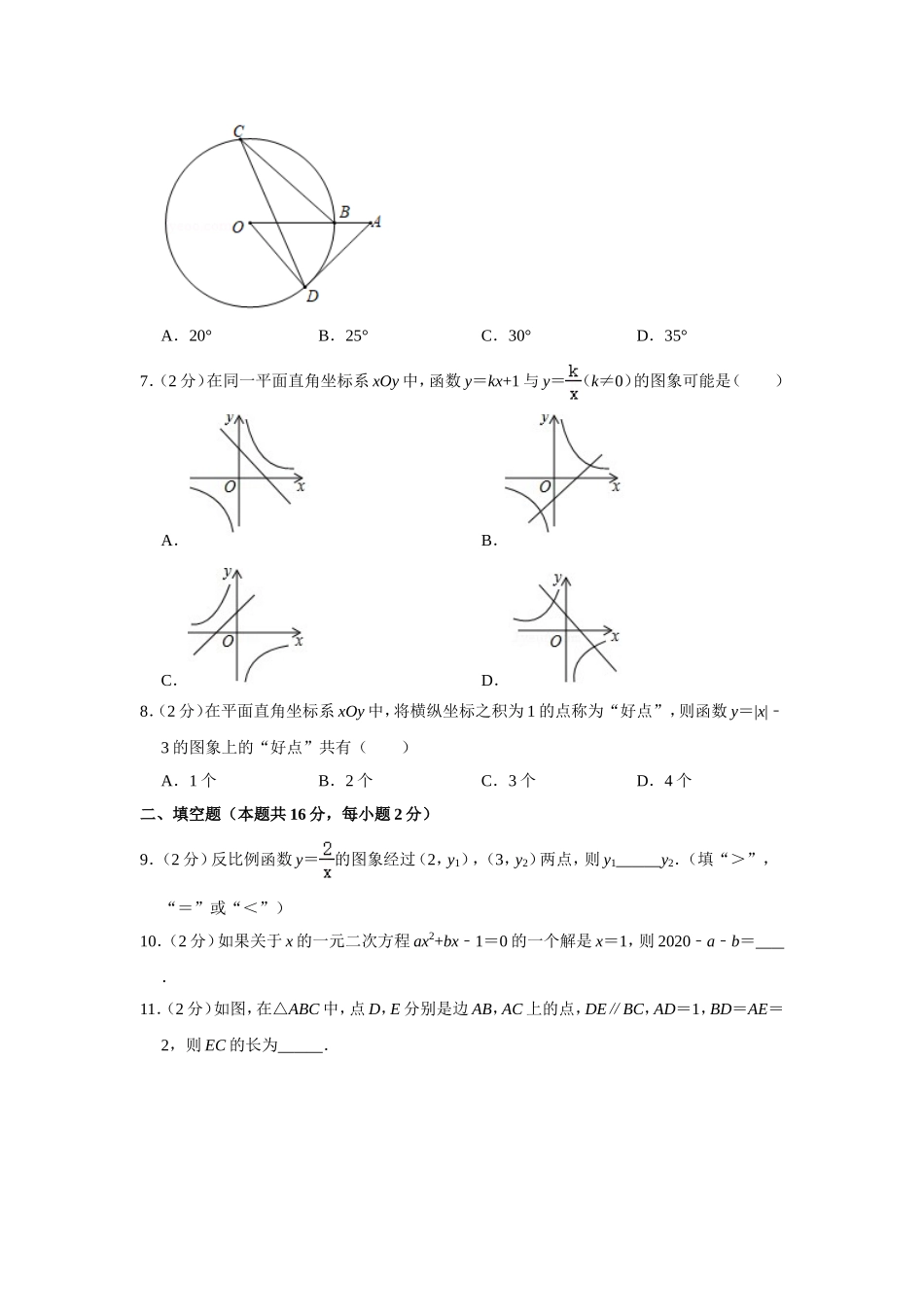
2019-2020学年北京市海淀区九年级(上)期末数学试卷一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.(2分)下列图形中既是轴对称图形,又是中心对称图形的是()A.B.C.D.2.(2分)五张完全相同的卡片上,分别写有数字1,2,3,4,5,现从中随机抽取一张,抽到的卡片上所写数字小于3的概率是()A.B.C.D.3.(2分)方程x2﹣3x﹣1=0的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法确定4.(2分)如图,在四边形ABCD中,AD∥BC,点E,F分别是边AD,BC上的点,AF与BE交于点O,AE=2,BF=1,则△AOE与△BOF的面积之比为()A.B.C.2D.45.(2分)若扇形的半径为2,圆心角为90°,则这个扇形的面积为()A.B.πC.2πD.4π6.(2分)如图,OA交⊙O于点B,AD切⊙O于点D,点C在⊙O上.若∠A=40°,则∠C为()A.20°B.25°C.30°D.35°7.(2分)在同一平面直角坐标系xOy中,函数y=kx+1与y=(k≠0)的图象可能是()A.B.C.D.8.(2分)在平面直角坐标系xOy中,将横纵坐标之积为1的点称为“好点”,则函数y=|x|﹣3的图象上的“好点”共有()A.1个B.2个C.3个D.4个二、填空题(本题共16分,每小题2分)9.(2分)反比例函数y=的图象经过(2,y1),(3,y2)两点,则y1y2.(填“>”,“=”或“<”)10.(2分)如果关于x的一元二次方程ax2+bx﹣1=0的一个解是x=1,则2020﹣a﹣b=.11.(2分)如图,在△ABC中,点D,E分别是边AB,AC上的点,DE∥BC,AD=1,BD=AE=2,则EC的长为.12.(2分)如图,在平面直角坐标系中有两点A(6,0)和B(6,3),以原点O为位似中心,相似比为,把线段AB缩短为线段CD,其中点C与点A对应,点D与点B对应,且CD在y轴右侧,则点D的坐标为.13.(2分)如表是某种植物的种子在相同条件下发芽率试验的结果.种子个数100400900150025004000发芽种子个数92352818133622513601发芽种子频率0.920.880.910.890.900.90根据表中的数据,可估计该植物的种子发芽的概率为.14.(2分)如图,⊙O是△ABC的外接圆,D是的中点,连结AD,BD,其中BD与AC交于点E.写出图中所有与△ADE相似的三角形:.15.(2分)如图,在平面直角坐标系xOy中,已知函数y1=(x>0)和y2=﹣(x<0),点M为y轴正半轴上一点,N为x轴上一点,过M作y轴的垂线分别交y1,y2的图象于A,B两点,连接AN,BN,则△ABN的面积为.16.(2分)如图,在...