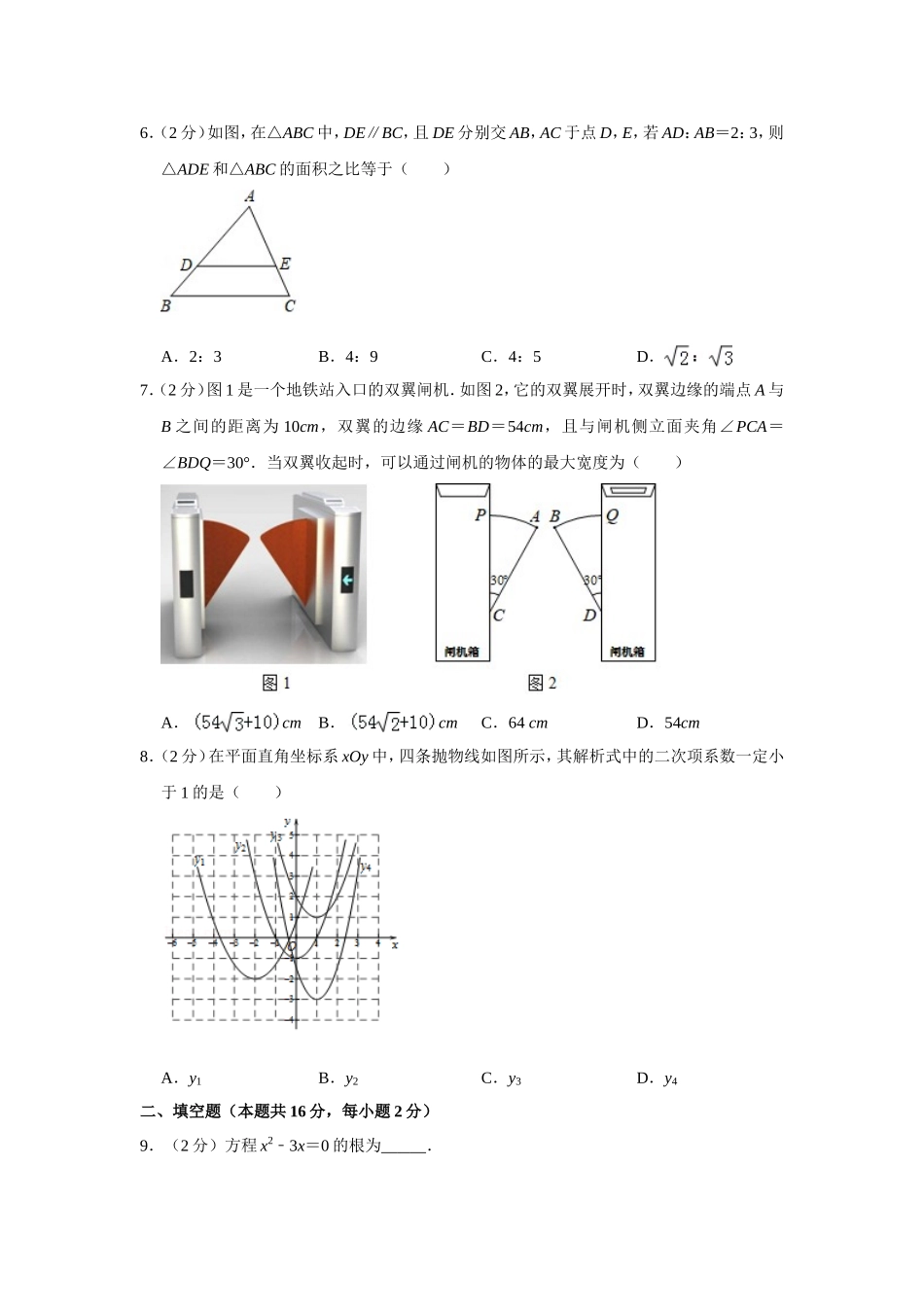
2018-2019学年北京市海淀区九年级(上)期末数学试卷一、选择题(本题共16分,每小题2分)下面各题均有四个选项,其中只有一个是符合题意的.请将正确选项前的字母填在表格中相应的位置.1.(2分)抛物线y=(x﹣1)2+3的顶点坐标是()A.(1,3)B.(﹣1,3)C.(1,﹣3)D.(3,﹣1)2.(2分)如图,在平面直角坐标系xOy中,点P(4,3),OP与x轴正半轴的夹角为α,则tanα的值为()A.B.C.D.3.(2分)方程x2﹣x+3=0的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.只有一个实数根4.(2分)如图,一块含30°角的直角三角板ABC绕点C顺时针旋转到△A'B'C,当B,C,A'在一条直线上时,三角板ABC的旋转角度为()A.150°B.120°C.60°D.30°5.(2分)如图,在平面直角坐标系xOy中,B是反比例函数y=(x>0)的图象上的一点,则矩形OABC的面积为()A.1B.2C.3D.46.(2分)如图,在△ABC中,DE∥BC,且DE分别交AB,AC于点D,E,若AD:AB=2:3,则△ADE和△ABC的面积之比等于()A.2:3B.4:9C.4:5D.7.(2分)图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为()A.cmB.cmC.64cmD.54cm8.(2分)在平面直角坐标系xOy中,四条抛物线如图所示,其解析式中的二次项系数一定小于1的是()A.y1B.y2C.y3D.y4二、填空题(本题共16分,每小题2分)9.(2分)方程x2﹣3x=0的根为.10.(2分)半径为2且圆心角为90°的扇形面积为.11.(2分)已知抛物线的对称轴是x=n,若该抛物线与x轴交于(1,0),(3,0)两点,则n的值为.12.(2分)在同一平面直角坐标系xOy中,若函数y=x与y=(k≠0)的图象有两个交点,则k的取值范围是.13.(2分)如图,在平面直角坐标系xOy中,有两点A(2,4),B(4,0),以原点O为位似中心,把△OAB缩小得到△OA'B'.若B'的坐标为(2,0),则点A'的坐标为.14.(2分)已知(﹣1,y1),(2,y2)是反比例函数图象上两个点的坐标,且y1>y2,请写出一个符合条件的反比例函数的解析式.15.(2分)如图,在平面直角坐标系xOy中,点A(3,0),判断在M,N,P,Q四点中,满足到点O和点A的距离都小于2的点是.16.(2分)如图,在平面直角坐标系xOy中,P是直线y=2上的一个动点,⊙P的半径为1,直线O...