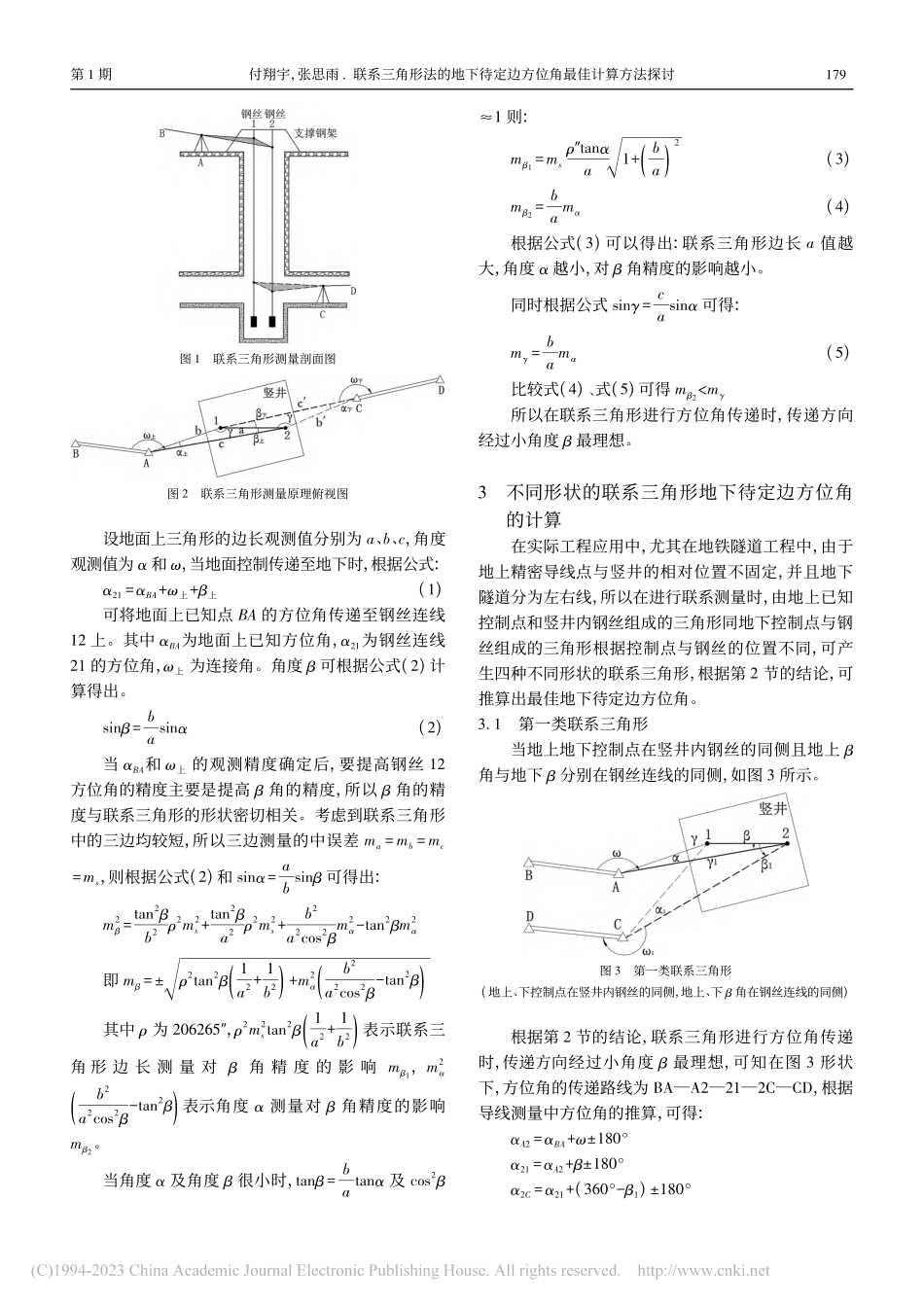
2023年2月第1期城市勘测UrbanGeotechnicalInvestigation&SurveyingFeb.2023No.1引文格式:付翔宇,张思雨.联系三角形法的地下待定边方位角最佳计算方法探讨[J].城市勘测,2023(1):178-181+186.文章编号:1672-8262(2023)01-178-05中图分类号:P258文献标识码:B联系三角形法的地下待定边方位角最佳计算方法探讨付翔宇*,张思雨*收稿日期:2022—03—24作者简介:付翔宇(1984—),男,硕士,高级工程师,主要从事工程测量、变形监测工作。E-mail:fuxiangyu_2002@163.com(中航勘察设计研究院有限公司,北京100098)摘要:在地下隧道工程施工过程中,为了保证隧道的正确贯通,需要将地面的控制系统精确地传递到地下工程中,本文将工程中常用的传递方法及其优缺点进行了总结,探讨了联系三角形的有利形状,给出了四类联系三角形情形下地下待定边方位角计算公式,并在实际工程中进行了检核,为类似工程应用中快速计算方位角提供了依据。关键词:联系测量;联系三角形法;地下待定边方位角计算1引言在城市轨道交通工程、矿山建设、管廊及其他地下暗挖工程中,为了保证开挖工程的正确贯通,需要将地面控制网中的坐标、方向及高程准确地传递至地下,使地上、地下采用同一坐标系统和高程系统,指导地下工程施工。这传递过程称为联系测量,包括平面联系测量和高程联系测量,联系测量的精度直接影响到地下工程的贯通精度,是实现地下工程贯通控制的核心与关键,其中高程联系测量一般通过垂吊钢尺的方法实现。根据地上平面控制导入地下的形式,平面联系测量方法有两井定向法、导线直接传递法、投点定向法、陀螺定向法和联系三角形法等。两井定向法原理为无定向导线,与一井定向相比,由于两吊垂线间的距离增大了,因而减小了投点误差引起的方向误差,有利于提高地下导线的精度,并且外业测量简单,占用竖井时间较短[4]。导线直接传递法采用精密导线测量的方法传递坐标和方位,一般适用于车站地下定向且施工场地比较开阔、地上地下通视良好的地段,并有较大的竖井(盾构工作井)或预留孔,此方法工作量不大、精准程度高,但是导线直传法的水平角观测具有边长很短、倾角很大、水平角值较小等特点[5]。投点定向法是通过地面钻孔或施工投料孔,用垂球或投点仪进行投点,将地面坐标和方位角传递到井下。此方法适用于埋深较浅、且已开挖一定长度的隧道。该方法具有操作简便、测量精度高、占用施工竖井时间少、对施工影响较小等优点,缺点是测量钻孔难度较大(垂直...