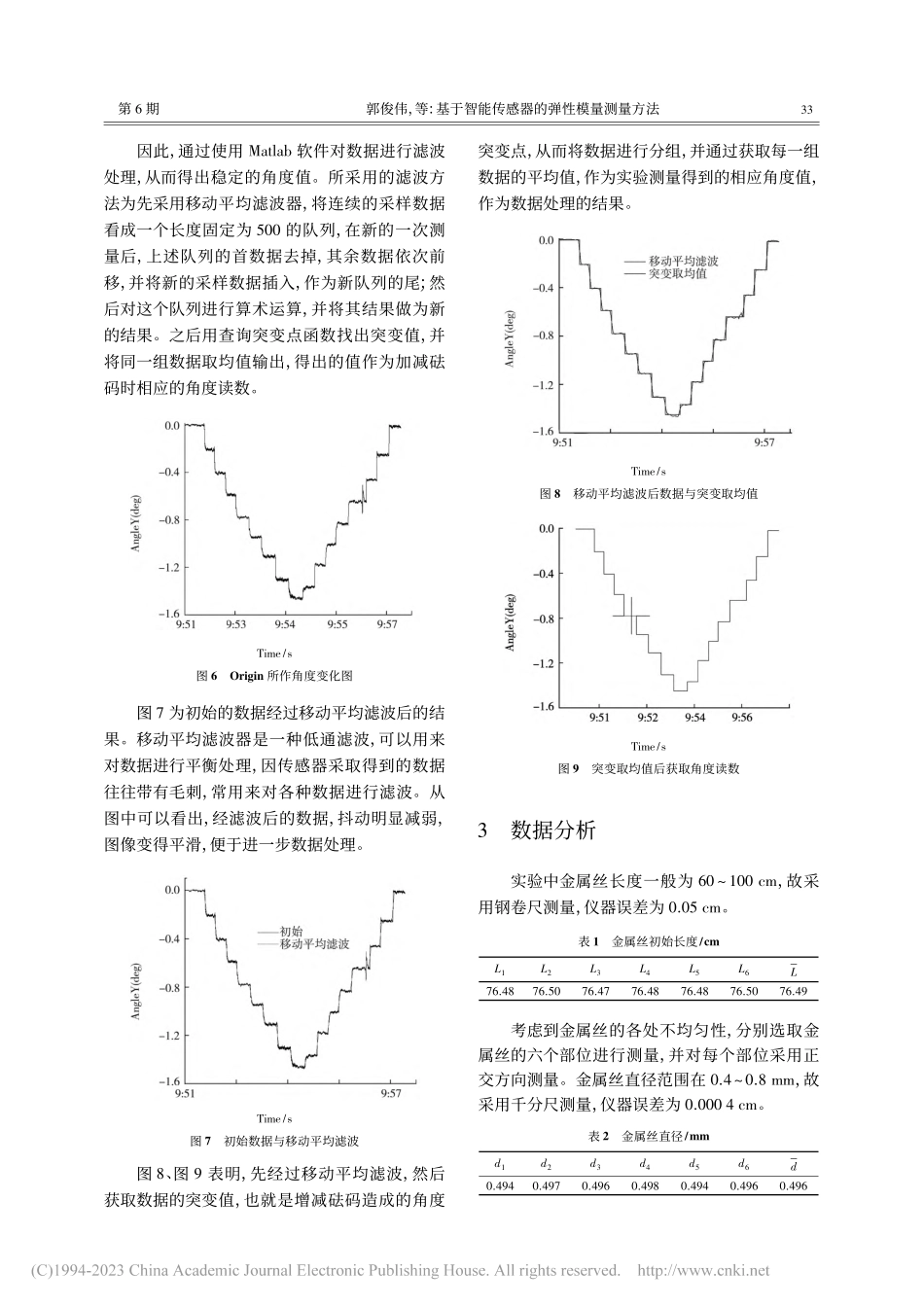
第35卷第6期大学物理实验Vol.35No.62022年12月PHYSICALEXPERIMENTOFCOLLEGEDec.2022收稿日期:2022-07-06基金项目:山东省本科教学改革研究项目(Z2021148、M2021284);山东建筑大学博士基金项目(X21088Z);山东建筑大学本科教学改革研究项目(XJG2021036)*通讯联系人文章编号:1007-2934(2022)06-0031-04基于智能传感器的弹性模量测量方法郭俊伟,王忠民,时术华,贺长伟*(山东建筑大学,山东济南250101)摘要:本文提出一种弹性模量测量方法,设计并3D打印制作测量支架,利用MEMS倾角传感器得到支架随金属丝形变旋转的微小角度的初始数据,通过Origin软件以及Matlab软件进行移动平均滤波以及差异点取均值算法得到测量角度,并根据三角函数关系得到测量金属丝在不同拉力下的长度形变量。根据拉伸法中弹性模量与形变量之间的对应关系,得到待测金属丝的弹性模量。实验结果测得的杨氏模量与理论值接近,相对不确定度约为5.49%。关键词:弹性模量;测量支架;MEMS倾角传感器;移动平均滤波;差异点取均值中图分类号:O4-33文献标志码:ADOI:10.14139/j.cnki.cn22-1228.2022.06.006弹性模量是描述固体材料抵抗形变能力的物理量,测定金属材料的杨氏弹性模量是大学物理实验中相关材料力学的基础性实验。静态拉伸法测金属形变量的方法很多,包括光学测量法的光杠杆法、莫尔条纹法、等厚干涉测量法、双缝干涉法、光纤传感器法等;以及电学测量法的直流双臂电桥法、惠斯通电桥法、RLC串联交流谐振法等[1]。国内大学普遍采用的方法为光杠杆法[2]。即在试样上施加一恒定的拉伸应力,利用光杠杆的放大原理测得金属丝的形变量,根据应力和应变计算弹性模量。该方法中光杠杆、尺读望远镜调节复杂性较高,光杠杆镜面和望远镜光轴初始角度以及在光线及视觉差等因素干扰下,读数误差较大[3,4]。目前提出一些新的改进方法,如在光杠杆的镜面旋转轴以及望远镜上各安装一个量角器,方便调节二者的角度以达到光杠杆镜面和望远镜光轴的严格垂直[5];采用光纤传感器代替光杠杆,精确测量金属丝的伸长量,从而测得金属的杨氏模量[6]等。随着微电子机械系统(MEMS)技术[7]的不断进步,MEMS倾角传感器所具备的体积小、性能高、以及低成本等优势,使得它在航空航天、工程机械以及消费电子等许多领域都有广泛的应用。经过调研,一些倾角传感器产品的角度测量分辨率甚至已达到0.0001°水平,完全可以满足实验室对微小角度的测量要求。实验中弹性模量测量时最关键的部分...