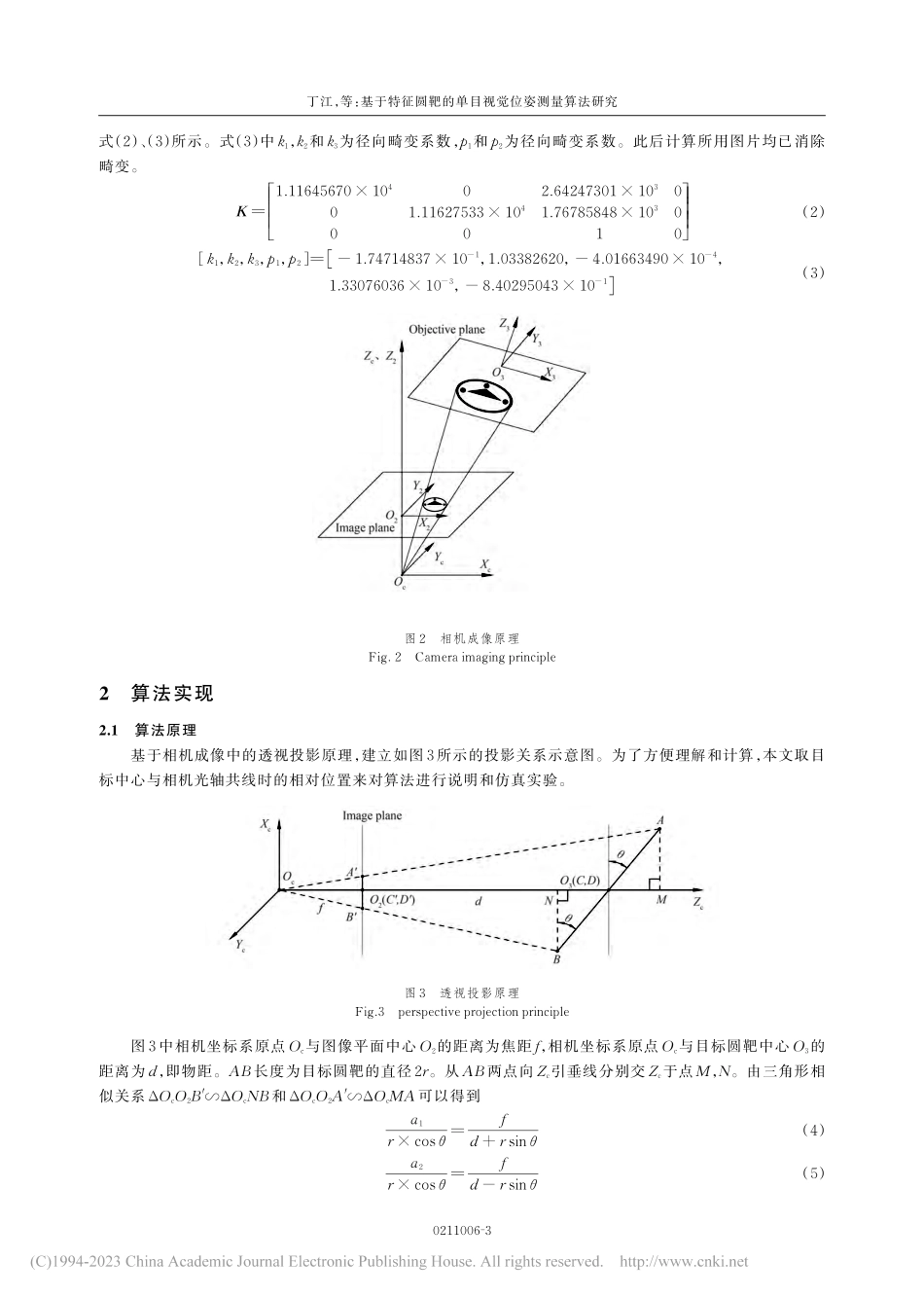
第52卷第2期2023年2月Vol.52No.2February2023光子学报ACTAPHOTONICASINICA0211006‑1基于特征圆靶的单目视觉位姿测量算法研究丁江1,宋朝成1,2,马翠2,何凯2,左启阳2(1广西大学机械工程院,南宁530004)(2中国科学院深圳先进技术研究院,深圳518055)摘要:为提高基于工业机器人近距离下空间平面位姿的求解精度,分析了由透视畸变引起的圆投影误差的变化规律,以物距与特征圆半径的比值作为衡量圆透视畸变误差的参数依据,提供了不同物距下的精度参考。推导了基于空间圆投影图像的三点相对位姿求解算法。定量的误差分析和实验验证表明,物距与特征圆半径比值在18以内像素精度在0.1~1像素时,算法精度平均可以达到0.1°,优于文中其他两种算法。关键词:测量;机器视觉;空间圆特征;位姿测量;透视投影中图分类号:TP391.41文献标识码:Adoi:10.3788/gzxb20235202.02110060引言随着工业机器人[1-2]的应用越来越广泛,基于机械臂的自动锁螺丝机器人[3],室内喷涂机器人[4],缺陷检测机器人[5]等的精度需求也越来越高,其中机械臂与工作平面的相对位姿的准确度往往是最为关键的一环。而圆作为生活中常见的几何特征,往往多出现于各种物体和工件之上。鉴于单目视觉位姿测量[6]较于双目、多目,具有结构简单,系统运算量低等优势,故研究基于平面圆特征的单目视觉系统下空间平面相对位姿的求解将具有重要意义。目前空间平面位姿求解主要分为多点约束问题和非点约束问题。前者主要有FISCHLERJ等[7]在1981年提出的基于点约束的多点透视问题(Perspectiven-pointsProblem,PnP),通过解析法和迭代法等可精确求解目标位姿,计算较为复杂;LEPRTITV等[8]提出的高效率多点透视(EfficientPerspectiven-pointsProblem,EPnP)算法在能获得高质量图像的前提下大大提升了PnP算法效率;陈鹏等[9]在EPnP算法基础上提出的基于迭代的高效率多点透视(IterativeEfficientPerspectiven-pointsProblem,IEPnP)算法,在对噪声的高鲁棒性下保持了EPnP算法的高效率。作为非点约束的基于平面圆特征的位姿测量研究因其靶标制作简易,原理简单,也引起了广大学者的注意。其基于是否考虑空间圆的透视畸变,又可分为考虑透视畸变的类椭圆方法和不考虑透视畸变的椭圆法。如KABUKAM和ARENASA[10]把圆投影图视作椭圆,提出了将投影椭圆短径与长径比值来作为目标平面的俯仰角,并通过目标靶面的投影阴影来消除姿态解的二义性。ZHOUZ等[11]在正投影的前...