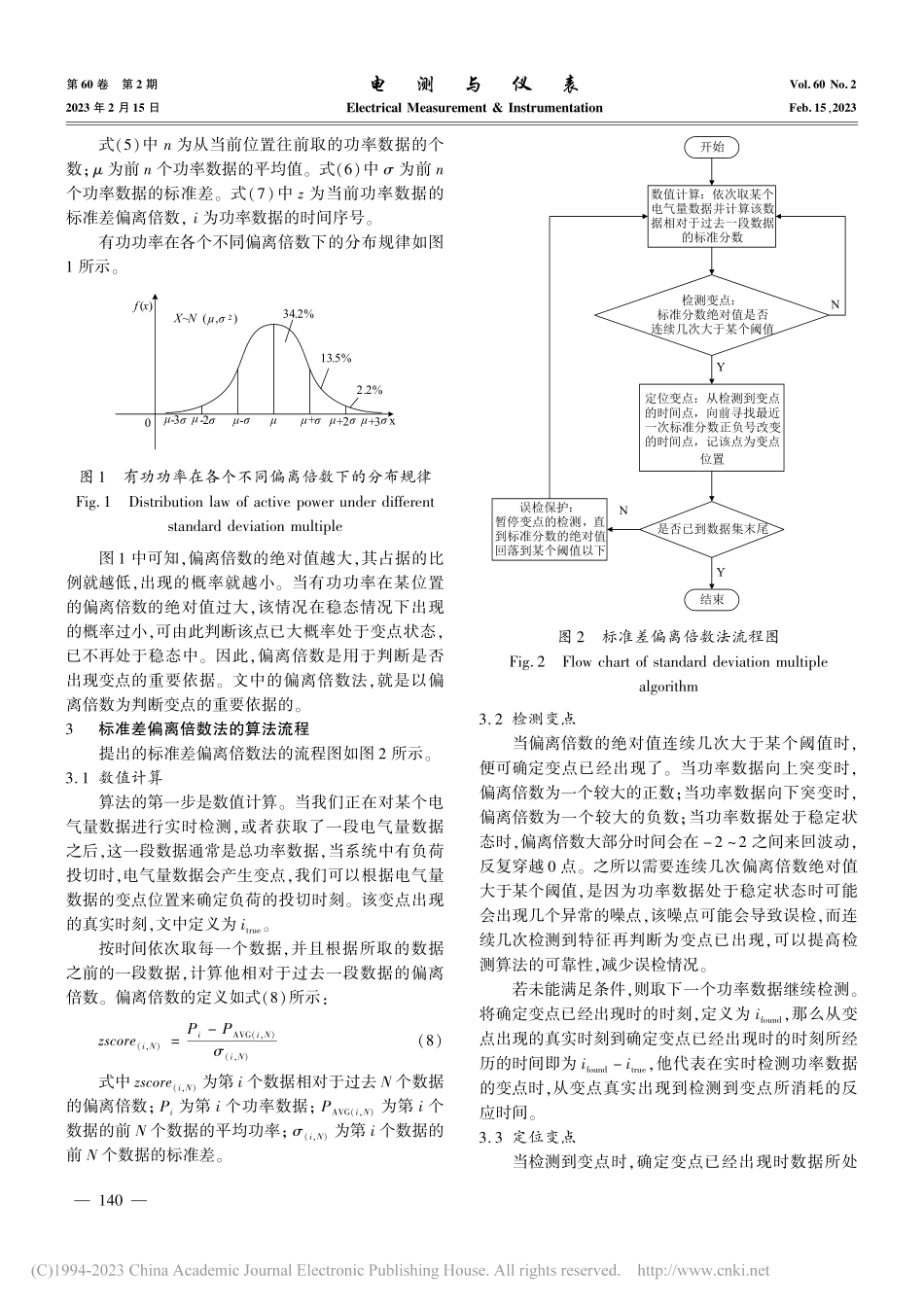
基于标准差偏离倍数的暂态事件检测算法张广龙,任建文,周明(华北电力大学,河北保定071003)摘要:暂态事件检测是非侵入式负荷监测的重要研究部分。然而已有的暂态事件检测方法需要已知投切负荷的有功功率跃变幅值,并依此设定功率跃变前后功率差的检测阈值,导致无法应用于多个有功功率跃变幅度不同的负荷同时投切的情况。为此,提出了一种基于标准差偏离倍数的暂态事件检测算法。该算法通过有功功率偏离均值相对于标准差的倍数来检测变点是否出现,并通过偏离倍数最近一次穿越零点的时刻来精确定位变点位置。通过仿真对比了偏离倍数法和滑动窗算法的检测速度和精度,用BLUED数据集验证了算法在多个不同特性负荷投切情况下的有效性。该算法相比已有的检测算法,不仅不需要设定功率跃变前后功率差的检测阈值,还能应用于多个不同特性负荷投切的情况。经测试该算法具有更好的检测速度、检测精度,较低的误检率和漏检率。关键词:变点检测;非侵入式负荷监测;BLUED数据集;算法统计特性DOI:10.19753/j.issn1001⁃1390.2023.02.020中图分类号:TM933文献标识码:B文章编号:1001⁃1390(2023)02⁃0138⁃09TransienteventdetectionalgorithmbasedonstandarddeviationmultipleZhangGuanglong,RenJianwen,ZhouMing(NorthChinaElectricPowerUniversity,Baoding071003,Hebei,China)Abstract:Transienteventdetectionisanimportantpartofnon⁃invasiveloadmonitoring.However,theexistingtransienteventdetectionmethodsneedtoknowtheactivepowerjumpamplitudeoftheloadswitching,andsetthedetectionthresh⁃oldofthepowerdifferencebeforeandafterthepowerjump,whichmakesitunabletobeappliedtomultipleloadswithdifferentactivepowerjumpamplitude.Therefo...