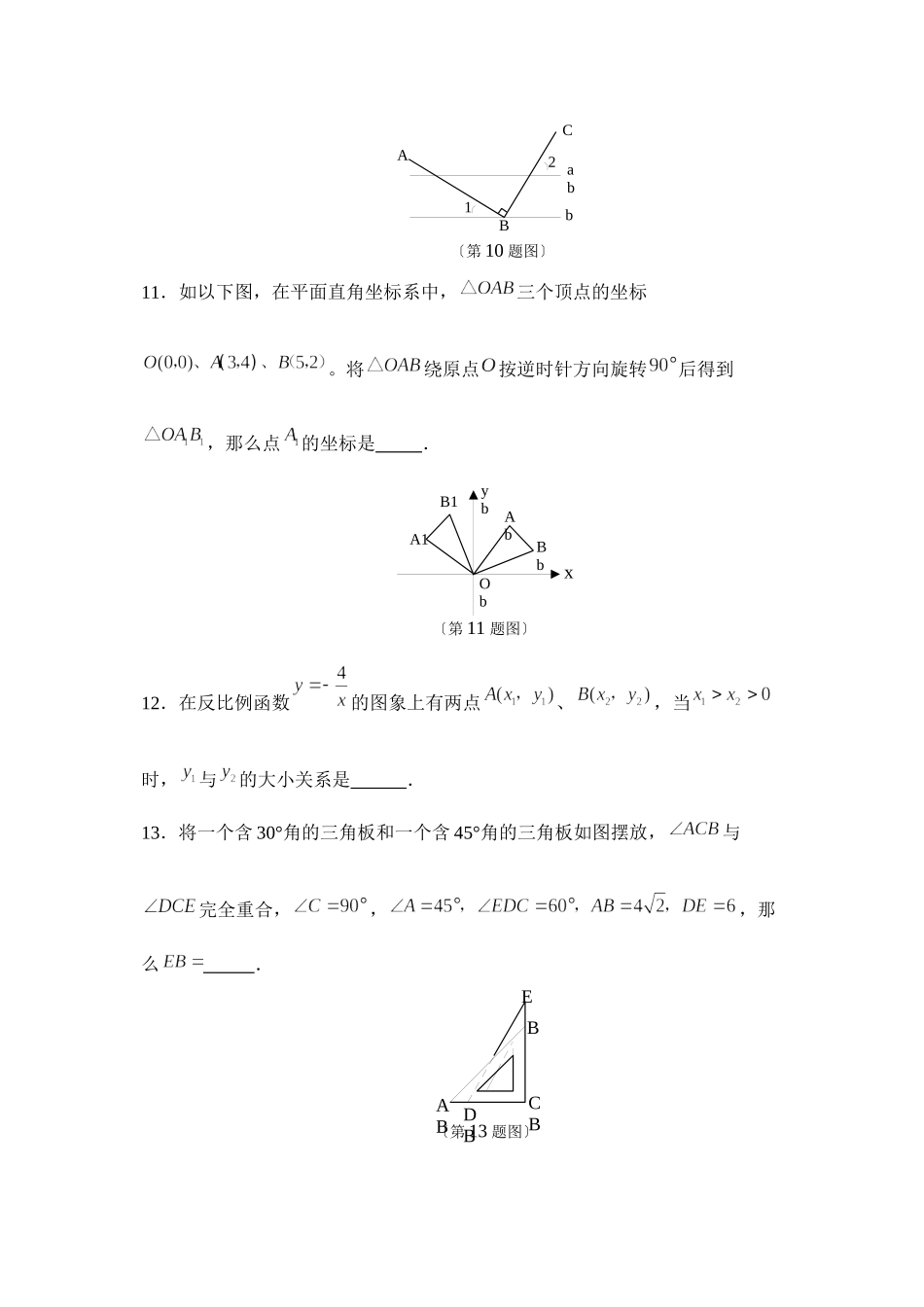
〔第3题图〕讲卫生防病毒2023年辽宁省抚顺市初中毕业生学业考试数学试卷考试时间120分钟试卷总分值150分一、选择题〔以下各题的备选答案中,只有一个是正确的.请将正确答案的选项填写在下表中相应题号下的空格内.每题3分,共24分〕1.的相反数是〔〕A.2B.C.D.2.某市在一次扶贫助残活动中,共捐款2580000元.将2580000元用科学记数法表示为〔〕A.元B.元C.元D.元3.一个正方体的每个面都有一个汉字,其平面展开图如以下图,那么在该正“方体中和毒〞字相对的字是〔〕A.卫B.防C.讲D.生4.以下事件是必然事件的是〔〕A.阴天一定会下雨B.翻开电视机,任选一个频道,屏幕上正在播放篮球比赛节目C.某种彩票的中奖率为1%,买100张彩票一定中奖D.13名学生中一定有两个人在同一个月过生日5.以下运算正确的选项是〔〕A.B.C.D.6.关于的二次函数,以下说法正确的选项是〔〕ADEPBCAFECB〔第7题图〕〔第8题图〕GA.图象的开口向上B.图象的顶点坐标是〔〕C.当时,随的增大而减小D.图象与轴的交点坐标为〔0,2〕7.如以下图,点分别是中边的中点,相交于点,,那么的长为〔〕A.4B.4.5C.5D.68.如以下图,正方形的面积为12,是等边三角形,点在正方形内,在对角线上有一点,使的和最小,那么这个最小值为〔〕A.B.C.3D.二、填空题〔每题3分,共24分〕9.一组数据4,3,5,,4,5的众数是4,那么.10.如以下图,直线,点在直线上,且,,那么度.ACBbab12〔第10题图〕ObBbAbybA1B1〔第11题图〕xEBCBDBAB〔第13题图〕11.如以下图,在平面直角坐标系中,三个顶点的坐标。将绕原点按逆时针方向旋转后得到,那么点的坐标是.12.在反比例函数的图象上有两点、,当时,与的大小关系是.13.将一个含30°角的三角板和一个含45°角的三角板如图摆放,与完全重合,,,那么.ABBBCBOB〔第14题图〕ABDBPBCBMBBB〔第15题图〕第1个图第2个图第3个图第4个图〔第16题图〕14.如以下图,圆锥的高为,底面圆的直径长为,那么此圆锥的侧面展开图的圆心角为度.15.如以下图,在梯形中,,点是线段上一定点,且=8.动点从点出发沿的路线运动,运动到点停止.在点的运动过程中,使为等腰三角形的点有个.16.观察以以下图形〔每幅图中最小的三角形都是全等的〕,请写出第个图中最小的三角形的个数有个.三、解答题〔每题8分,共16分〕1009080706050403020100球类跳绳踢毽其它类别304080人数图②〔第19题图〕图①球类40%跳绳其它踢毽15%17.计算:....