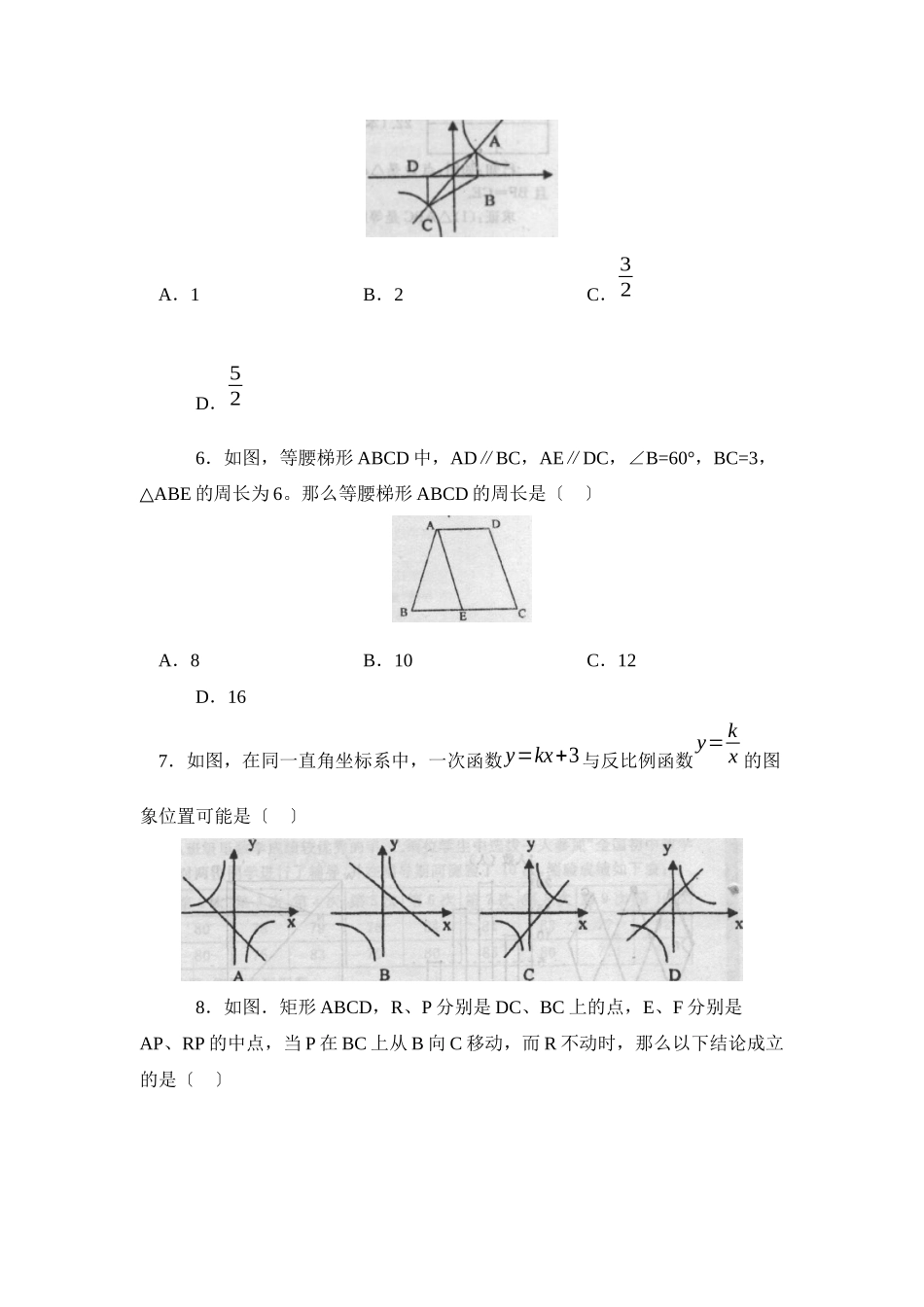
2023学年度德州市禹城第二学期八年级期末教学质量检测数学试题〔总分值120分考试时间120分钟〕一、选择题〔每个小题3分,共24分〕1.分式1x−3专有意义,那么x的取值范围是〔〕A.x>3B.x<3C.x≠3D.x≠-32.分式x2y−x−y2y−x的结果是〔〕A.−y−xB.y−xC.x−yD.x+y3.四边形ABCD,仅从以下条件中任取两个加以组合,使得四边形ABCD是平行四边形,一共有多少种不同的组合〔〕AB//CD①;②BC//AD;③AB=CD;④BC=ADA.2组B.3组C.4组D.6组4.某品牌服装销售商对各种型号服装的市场占有率进行调查时,他最应该关注的是服装型号的〔〕A.平均数B.众数C.中位数D.极差5.正比例函数y=x与反比例函数y=1x的图象相交于点A、C,AB⊥x轴于B,CD⊥轴于D,那么四边形ABCD的面积为〔〕A.1B.2C.32D.526.如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠B=60°,BC=3,△ABE的周长为6。那么等腰梯形ABCD的周长是〔〕A.8B.10C.12D.167.如图,在同一直角坐标系中,一次函数y=kx+3与反比例函数y=kx的图象位置可能是〔〕8.如图.矩形ABCD,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当P在BC上从B向C移动,而R不动时,那么以下结论成立的是〔〕A.线段EF的长逐渐增大B.线段EF的长逐渐减小C.线段EF的长不改变D.线段EF的长不能确定二、填空题〔每题3分,共30分〕9.分式x2−1x+1的值为0,那么x=_____________.10.化简(ab−ba)÷a+ba=____________.11.反比侧函数y=−8x的图象经过点P〔a+1,4〕,那么a=__________.12.点A〔-2,a〕,B〔-l,b〕,C〔3,c〕在双曲线y=kx(k<0)上,那么a、b、c的大小关系为_________________“.〔用<〞连接〕13.一组数据9,9,x,7的平均数与众数恰好相等,那么这组数据的中位数是________________.14.,等腰梯形ABCD中,AD//BC,对角线ACBD⊥,AD=3cm,BC=7cm,那么梯形的高是_____________cm.15.在四边形ABCD中,AB∥CD,假设加上AD∥BC,那么四边形ABCD为平行四边形.现在请你添加一个适当的条件:_________________________________,使得四边形AECF为平行四边形.〔图中不再添加点和线〕16.如图,是根据四边形的不稳定性制作的边长为10cm的可活动的菱形衣架,假设墙上钉子间的距离AB=BC=10cm,那么∠1=__________度.17.小强对班级50名同学在假期中阅读课外书数量的情况进行调查,并绘制了统计图〔如以下图〕,根据统计图可知,该班同学阅读课外书数量的极差是______________,中位数是_____...