2023年高考数学试题汇编及年高考模拟试题汇编三角函数及三角恒等变换（60页）高中数学.docxVIP免费

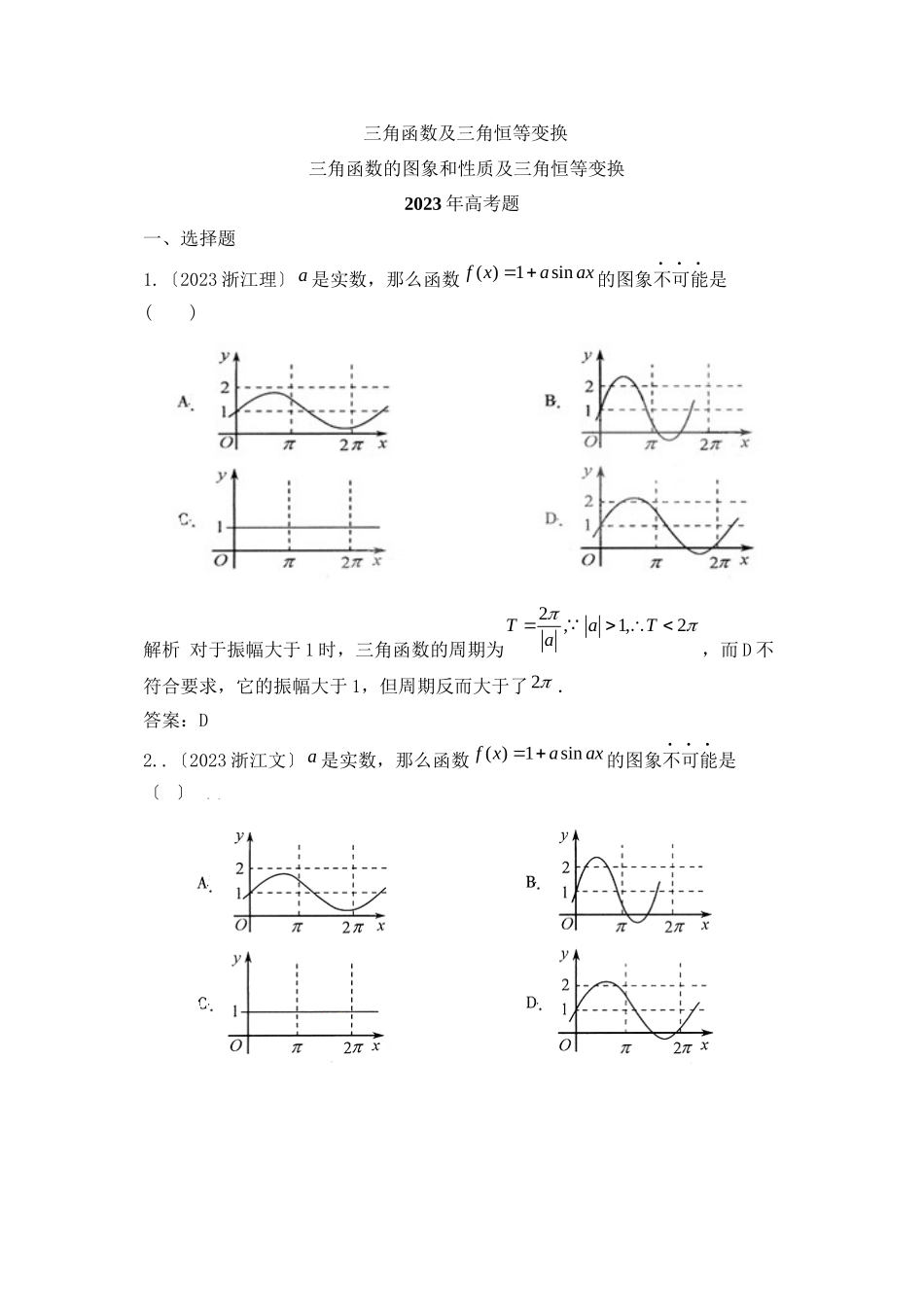
三角函数及三角恒等变换三角函数的图象和性质及三角恒等变换2023年高考题一、选择题1.〔2023浙江理〕是实数，那么函数的图象不可能是()解析对于振幅大于1时，三角函数的周期为，而D不符合要求，它的振幅大于1，但周期反而大于了．答案：D2..〔2023浙江文〕是实数，那么函数的图象不可能是〔〕a()1sinfxaax2,1,2TaTa2a()1sinfxaax【命题意图】此题是一个考查三角函数图象的问题，但考查的知识点因含有参数而丰富，结合图形考查使得所考查的问题形象而富有深度．【解析】对于振幅大于1时，三角函数的周期为，而D不符合要求，它的振幅大于1，但周期反而大于了．答案D3.(2023山东卷理)将函数的图象向左平移个单位,再向上平移1个单位,所得图象的函数解析式是().A.B.C.D.解析将函数的图象向左平移个单位,得到函数即的图象,再向上平移1个单位,所得图象的函数解析式为,应选B.答案:B【命题立意】:此题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的根本知识和根本技能,学会公式的变形.4.(2023山东卷文)将函数的图象向左平移个单位,再向上平移1个单位,所得图象的函数解析式是().2,1,2TaTa2sin2yx4cos2yx22cosyx)42sin(1xy22sinyxsin2yx4sin2()4yxsin(2)cos22yxx21cos22cosyxxsin2yx4A.B.C.D.解析将函数的图象向左平移个单位,得到函数即的图象,再向上平移1个单位,所得图象的函数解析式为,应选A.答案:A【命题立意】:此题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的根本知识和根本技能,学会公式的变形.5.(2023年广东卷文)函数是A．最小正周期为的奇函数B.最小正周期为的偶函数C.最小正周期为的奇函数D.最小正周期为的偶函数解析因为为奇函数,,所以选A.答案A6.〔2023全国卷Ⅰ理〕如果函数的图像关于点中心对称，那么的最小值为〔〕22cosyx22sinyx)42sin(1xycos2yxsin2yx4sin2()4yxsin(2)cos22yxx21cos22cosyxx1)4(cos22xy2222cos()1cos2sin242yxxx22Tcos2yx＝3＋43，0||A.B.C.D.解析:函数的图像关于点中心对称由此易得.应选C答案C7.〔2023全国卷Ⅰ理〕假设，那么函数的最大值为。解析:令,答案8〔2023安徽卷理〕函数，的图像与直线的两个相邻交点的距离等于，那么的单调递增区间是A.B.C.D.解析，由题...